Exercise 3.2.1. a) Consider the vectors  and
and 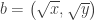 where
where  and
and  are arbitrary positive real numbers. Use the Schwarz inequality involving
are arbitrary positive real numbers. Use the Schwarz inequality involving  and
and  to derive a relationship between the arithmetic mean
to derive a relationship between the arithmetic mean 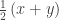 and the geometric mean
and the geometric mean  .
.
b) Consider a vector from the origin to point  , a second vector of length
, a second vector of length 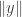 from
from  to the point
to the point 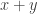 and the third vector from the origin to
and the third vector from the origin to 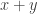 . Using the triangle inequality
. Using the triangle inequality

derive the Schwarz inequality. (Hint: Square both sides of the inequality and expand the expression  .)
.)
Answer: a) From the Schwarz inequality we have

From the definitions of  and
and  , on the left side of the inequality we have
, on the left side of the inequality we have


assuming we always choose the positive square root.
From the definitions of  and
and  we also have
we also have

and

so that the right side of the inequality is
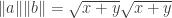

again assuming we choose the positive square root. (We know 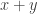 is positive since both
is positive since both  and
and  are.)
are.)
The Schwartz inequality

then becomes

or (dividing both sides by 2)
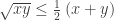
We thus see that for any positive real numbers  and
and  the geometric mean
the geometric mean  is less than the arithmetic mean
is less than the arithmetic mean 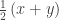 .
.
b) From the triangle inequality we have

for the vectors  and
and  . Squaring the term on the left side of the inequality and using the commutative and distributive properties of the inner product we obtain
. Squaring the term on the left side of the inequality and using the commutative and distributive properties of the inner product we obtain

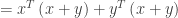
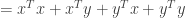
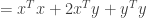

Squaring the term on the right side of the inequality we have

The inequality

is thus equivalent to the inequality
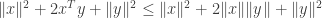
Subtracting 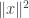 and
and 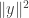 from both sides of the inequality gives us
from both sides of the inequality gives us

and dividing both sides of the inequality by 2 produces

Note that this is almost but not quite the Schwarz inequality: Since the Schwarz inequality involves the absolute value  we must also prove that
we must also prove that

(After all, the inner product 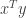 might be negative, in which case the inequality
might be negative, in which case the inequality  would be trivially true, given that the term on the right side of the inequality is guaranteed to be positive.)
would be trivially true, given that the term on the right side of the inequality is guaranteed to be positive.)
We have 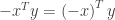 . Since the triangle inequality holds for any two vectors we can restate it in terms of
. Since the triangle inequality holds for any two vectors we can restate it in terms of 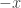 and
and  as follows:
as follows:
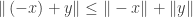
Since  squaring the term on the right side of the inequality produces
squaring the term on the right side of the inequality produces

as it did previously. However squaring the term on the left side of the inequality produces
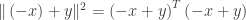
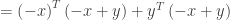


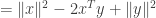
The original triangle inequality
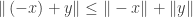
is thus equivalent to

or

Since we have both  and
and  we therefore have
we therefore have

which is the Schwarz inequality.
So the triangle inequality implies the Schwarz inequality.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
 Buy me a snack to sponsor more posts like this!
Buy me a snack to sponsor more posts like this!
,
,
, and
, and the center (carbon atom) at
. What is the cosine of the angle between the rays going from the center to each of the vertices?
be the ray from
to
and
be the ray from
to
. We have
between
and
as
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.

