My Math Homework

Linear Algebra and Its Applications, Exercise 2.6.2

Posted on April 6, 2013 by hecker

Exercise 2.6.2. Specify the 2 by 2 matrix that has the following effects:

projecting all vectors onto the $x$ axis
projecting the resulting vectors onto the $y$ axis

Answer: From the discussion in the first part of section 2.6 we know that the matrix

$\begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix}$

will project vectors onto the $x$ axis.

Similarly the matrix

$\begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix}$

will project vectors onto the $y$ axis.

To accomplish both operations in succession we therefore need to multiply vectors by the first matrix and then by the second; this corresponds to multiplying vectors by the product matrix

$\begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix} \begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix} = \begin{bmatrix} 0&0 \\ 0&0 \end{bmatrix}$

Note that the resulting matrix projects all vectors onto the origin.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.6.1

Posted on March 31, 2013 by hecker

Exercise 2.6.1. Specify the 2 by 2 matrix that has the following effects:

Rotating all vectors 90 degrees.
Projecting the resulting vectors onto the $x$ axis.

Answer: From the discussion in the first part of section 2.6 we know that the matrix

$\begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix}$

will rotate vectors through 90 degrees. From the same discussion we know that the matrix

$\begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix}$

will project vectors onto the $x$ axis.

To accomplish both operations in succession we therefore need to multiply vectors by the first matrix and then by the second; this corresponds to multiplying vectors by the product matrix

$\begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix} \begin{bmatrix} 0&-1 \\ 1&0 \end{bmatrix} = \begin{bmatrix} 0&-1 \\ 0&0 \end{bmatrix}$

For example, this matrix will take the vector $(1, 1)$ and transform it into the vector $(-1, 0)$

$\begin{bmatrix} 0&-1 \\ 0&0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -1 \\ 0 \end{bmatrix}$

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.19

Posted on March 24, 2013 by hecker

Exercise 2.5.19. Verify that Euler’s formula (nodes – edges + loops = 1) is valid for a square mesh with 10 nodes on each side.

Answer: If the mesh has 10 nodes on each side there are 10 times 10 or 100 nodes in total.

A given side has 9 edges between the 10 nodes on that side. There are 10 times 9 or 90 vertical edges, and 10 times 9 or 90 horizontal edges, for a total of 180 edges.

There are 9 times 9 or 81 independent loops.

We thus have the number of nodes minus the number of edges plus the number of loops equal to 100 – 180 + 81 = 1, in accordance with Euler’s formula.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.18

Posted on March 17, 2013 by hecker

Exercise 2.5.18. Consider a directed graph of $n$ nodes, where every node has a edge connecting it to every other node. How many edges are in this complete graph?

Answer: Each of the $n$ nodes has a connection to the $n-1$ other nodes. This would normally produce a total of $n(n-1)$ connections; however in order to avoid double counting a given edge we have to divide this value by 2. (In other words an edge from node $i$ to node $j$ counts as a connection for both nodes.) The total number of edges in the complete graph is therefore $n(n-1)/2$ .

For example, a 2-node complete graph has $2 \cdot (2-1)/2 = 2/2 = 1$ edge, a 3-node complete graph has $3 \cdot (3-1)/2 = 6/2 = 3$ edges, a 4-node complete graph has $4 \cdot (4-1)/2 = 12/2 = 6$ edges, and so on.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.17

Posted on March 10, 2013 by hecker

Exercise 2.5.17. In the scheme described in section 2.5 for ranking football teams, is strength of opposition accounted for, or must it be considered separately?

Answer: The ranking system described calculates potential values for each team based on score differences for the games each team plays. Consider the situation where the graph of teams is not connected; in other words, at least one group of teams has games only among members of the group, with teams in the group never playing teams in other groups. (For example, consider a football conference in which the teams never play non-conference games.)

In that case the calculated potentials can be used to rank teams within the group, but cannot be used to rank a team within the group relative to a team outside the group, or vice versa. If you wanted to create a ranking of all teams then you would have to explicitly incorporate some measure of the strength of the opposition, e.g., based on subjective assessments of the talent of the teams in each conference.

However if the graph is connected then the estimated potential for a team should already reflect the relative strength of the team’s opponents. Consider the following simple example with four teams (1 through 4):

Team 1 defeats team 2, 14-8.
Team 2 defeats team 3, 27-18.
Team 4 defeats team 3, 14-0.

If we assume that in each case the winning team is the home team, this corresponds to the incidence matrix

$A = \begin{bmatrix} 1&-1&0&0 \\ 0&1&-1&0 \\ 0&0&-1&1 \end{bmatrix}$

with the system $Ax = b$ expressed in matrix form as

$Ax = \begin{bmatrix} 1&-1&0&0 \\ 0&1&-1&0 \\ 0&0&-1&1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 6 \\ 9 \\ 14 \end{bmatrix}$

where 6, 9, and 14 are the respective differences in the scores. This in turn corresponds to the system of equations

$\begin{array}{rcrcrcrcr} x_1&-&x_2&&&&&=&6 \\ &&x_2&-&x_3&&&=&9 \\ &&&&-x_3&+&x_4&=&14 \end{array}$

If we arbitrarily ground the network at team 4 by setting $x_4 = 0$ then from the third equation we have $x_3 = -14$ . Substituting the value of $x_3$ into the second equation we have $x_2 = -5$ . Finally, substituting the value of $x_2$ into the first equation we have $x_1 = 1$ .

Note that team 1 (with potential $x_1 = 1$ ) is ranked higher than team 4 (with potential $x_4 = 0$ ) even though team 4 won its game against team 3 in a more convincing fashion. That’s because based on the game results team 1’s opponent team 2 is considered a stronger opponent than team 4’s opponent team 3, and team 1 won its game with just enough points to have its calculated potential be higher than that of team 4.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | 2 Comments

Linear Algebra and Its Applications, Exercise 2.5.16

Posted on March 3, 2013 by hecker

Exercise 2.5.16. Suppose we have a directed graph with four nodes and five edges as follows:

edge 1 from node 1 to node 2
edge 2 from node 2 to node 3
edge 3 from node 1 to node 3
edge 4 from node 1 to node 4
edge 5 from node 3 to node 4

Also assume that the graph is grounded at node 4. Do the following:

Describe the current laws $A^Ty = 0$ at the three ungrounded nodes 1, 2, and 3.
Describe how the current law at the grounded node 4 follows from the current laws at the other three nodes.
Specify the rank of $A^T$ .
Relate the solutions to $A^Ty = 0$ to the loops in the graph.

Answer: We start by constructing the incidence matrix for the network; it contains 5 rows corresponding to the edges and 4 columns corresponding to the nodes:

$A = \begin{bmatrix} -1&1&0&0 \\ 0&-1&1&0 \\ -1&0&1&0 \\ -1&0&0&1 \\ 0&0&-1&1\end{bmatrix}$

The system $A^Ty = 0$ can be expressed in matrix form as

$\begin{bmatrix} -1&0&-1&-1&0 \\ 1&-1&0&0&0 \\ 0&1&1&0&-1 \\ 0&0&0&1&1 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$

a) The equations corresponding to the current laws for the first three (ungrounded) nodes are

$\begin{array}{rcrcrcrcrcrcr} -y_1&&&-&y_3&-&y_4&&&=&0 \\ y_1&-&y_2&&&&&&&=&0 \\ &&y_2&+&y_3&&&-&y_5&=&0 \end{array}$

b) The equation for the current law at the grounded node is $y_4+y_5=0$ . It can be derived from the three equations above by adding the first equation to the second equation to produce the equation $-y_2-y_3-y_4 = 0$ and then adding this equation to the third equation to produce $-y_4-y_5=0$ or $y_4+y_5=0$ .

c) From inspection $A^T$ appears to have three pivots (in columns 1, 2, and 4) and therefore has rank 3. We can confirm this via elimination:

$\begin{bmatrix} -1&0&-1&-1&0 \\ 1&-1&0&0&0 \\ 0&1&1&0&-1 \\ 0&0&0&1&1 \end{bmatrix} \Rightarrow \begin{bmatrix} -1&0&-1&-1&0 \\ 0&-1&-1&-1&0 \\ 0&1&1&0&-1 \\ 0&0&0&1&1 \end{bmatrix}$

$\Rightarrow \begin{bmatrix} -1&0&-1&-1&0 \\ 0&-1&-1&-1&0 \\ 0&0&0&-1&-1 \\ 0&0&0&1&1 \end{bmatrix} \Rightarrow \begin{bmatrix} -1&0&-1&-1&0 \\ 0&-1&-1&-1&0 \\ 0&0&0&-1&-1 \\ 0&0&0&0&0 \end{bmatrix}$

As noted above, there are three pivots in columns 1, 2, and 4, and thus the rank of $A^T$ is 3.

d) From the elimination above we see that $y_1$ , $y_2$ , and $y_4$ are basic variables and $y_3$ and $y_5$ are free variables. The resulting echelon matrix corresponds to the following system of equations:

$\begin{array}{rcrcrcrcrcrcr} -y_1&&&-&y_3&-&y_4&&&=&0 \\ &&-y_2&-&y_3&-&y_4&&&=&0 \\ &&&&&&-y_4&-&y_5&=&0 \end{array}$

If we set $y_3 =1$ and $y_5 = 0$ then from the third equation we have $y_4 = 0$ . Substituting into the second equation we have $y_2 = -1$ . Substituting into the first equation we have $y_1 = -1$ .

If we set $y_3 =0$ and $y_5 = 1$ then from the third equation we have $y_4 = -1$ . Substituting into the second equation we have $y_2 = 1$ . Substituting into the first equation we have $y_1 = 1$ .

The general solution to $A^Ty = 0$ is thus given by

$y_3 \begin{bmatrix} -1 \\ -1 \\ 1 \\ 0 \\ 0 \end{bmatrix} + y_5 \begin{bmatrix} 1 \\ 1 \\ 0 \\ -1 \\ 1 \end{bmatrix}$

The first term can be interpreted as a set of currents around the upper loop in the graph: In the bottom edge we have a current of $y_3$ from node 1 to node 3. We then have a current of $-y_3$ from node 2 to node 3, equivalent to a current of $y_3$ from node 3 to node 2. Finally we have a current of $-y_3$ from node 1 to node 2, equivalent to a current of $y_3$ from node 2 to node 1. The net current around the loop is zero.

The second term can be interpreted as a set of currents around the outer loop in the graph: In the top left edge we have a current of $y_5$ from node 1 to node 2. We then have a current of $y_5$ from node 2 to node 3 along the upper right edge, and a current of $y_5$ from node 3 to node 4 along the bottom right edge. Finally we have a current of $-y_5$ from node 1 to node 4, equivalent to a current of $y_5$ from node 4 to node 1. Again the net current around the loop is zero.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.15

Posted on February 24, 2013 by hecker

Exercise 2.5.15. Suppose that MIT, Harvard, Yale, and Princeton compete in some sport, with MIT beating Harvard 35-0, Yale and Harvard playing to a tie, and Princeton beating Yale 7-6. What score differences in the other three possible games (MIT-Yale, MIT-Princeton, and Harvard-Princeton) would allow potential differences agreeing with the score differences?

Answer: We can consider this as a graph with four nodes (M, H, Y, and P) and six edges. Note that we can picture the nodes arranged in a square, with the edges M-H, H-Y, and Y-P forming three of the outside edges of the square, P-M forming the fourth outside edge, and Y-M and P-H being the diagonals. Note that we assume that each edge goes from the visiting team to the home team; thus, for example, the edge M-H represents a game played by MIT at Harvard.

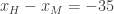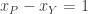The scores provided correspond to potential differences between the nodes, more specifically the potential of the home team minus the potential of the visiting team, which in our model corresponds to the score difference between the teams. Thus the potential difference $x_H - x_M = -35$ , the potential difference $x_Y-x_H=0$ , and the potential difference $x_P - x_Y = 1$ .

The total potential differences around any loop must sum to 0; in particular this is true for the outer loop formed by the four edges of the square, so that

$(x_M - x_P) + (x_H-x_M) + (x_Y-x_H) + (x_P-x_Y) = 0$

$\rightarrow (x_M - x_P) -35 +0 +1 = 0 \rightarrow (x_M - x_P) = 34$

This potential difference is consistent with MIT beating Princeton by a score of 34-0, or 41-7, or any other score where MIT wins by 34 points.

Around the inner loop formed by the edges M-H, H-Y, and Y-M we have

$(x_M - x_Y) + (x_H-x_M) + (x_Y-x_H) = 0$

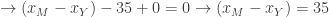
$\rightarrow (x_M - x_Y) -35+0 = 0 \rightarrow (x_M - x_Y) = 35$

This potential difference is consistent with MIT beating Yale by a score of 35-0, or 44-9, or any other score where MIT wins by 35 points.

Finally, around the inner loop formed by the edges P-H, H-Y, and Y-P we have

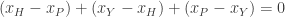
$(x_H - x_P) + (x_Y-x_H) + (x_P-x_Y) = 0$

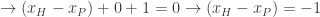
$\rightarrow (x_H - x_P) +0+1 = 0 \rightarrow (x_H - x_P) = -1$

This potential difference is consistent with Princeton beating Harvard by a score of 7-6, or 14-13, or any other score where Princeton wins by 1 point.

Note also that the three edges M-H, H-Y, and Y-P form a spanning tree, since they connect all four nodes, and the score differences along those edges determine the score differences along all the other edges. This is true in general: If a set of edges forms a spanning tree, then the potential differences along those edges determine the potential differences along all other edges.

This occurs because a spanning tree is a graph that connects all the nodes but that has no loops. If another edge is added then that will form a loop where previously there was none, and since the potential differences around the new loop must sum to 0, the potential differences along the new edge are determined by the potential differences along the edges previously in the spanning tree.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.14

Posted on February 17, 2013 by hecker

Exercise 2.5.14. Suppose we have the block matrices

$\begin{bmatrix} A&B \\ C&D \end{bmatrix} \begin{bmatrix} E&F \\ G&H \end{bmatrix}$

with the following properties:

$A$ and $B$ have $m_1$ rows
$C$ and $D$ have $m_2$ rows
$E$ and $F$ have $n_1$ rows
$G$ and $H$ have $n_2$ rows
$E$ and $H$ are square matrices

What is the product of the two matrices, and what are the sizes of each of the product’s component submatrices?

Answer: Since $E$ is a square matrix with $n_1$ rows it must have $n_1$ columns. If $E$ has $n_1$ columns then $G$ must have $n_1$ columns also. Similarly, since $H$ is a square matrix with $n_2$ rows it must have $n_2$ columns, and $F$ must have $n_2$ columns as well.

In computing the (1, 1) element of the product matrix we multiply $A$ by $E$ and $B$ by $G$ . (See the post on multiplying block matrices.) This means that the number of columns of $A$ must equal the number of rows of $E$ or $n_1$ , and the number of columns of $B$ must equal the number of rows of $G$ or $n_2$ . The number of columns of $C$ and $D$ must then be $n_1$ and $n_2$ respectively.

The sizes of each of the elements $A$ through $H$ is thus as follows:

$A$ is $m_1$ by $n_1$
$B$ is $m_1$ by $n_2$
$C$ is $m_2$ by $n_1$
$D$ is $m_2$ by $n_2$
$E$ is $n_1$ by $n_1$
$F$ is $n_1$ by $n_2$
$G$ is $n_2$ by $n_1$
$H$ is $n_2$ by $n_2$

The product matrix is thus

$\begin{bmatrix} A&B \\ C&D \end{bmatrix} \begin{bmatrix} E&F \\ G&H \end{bmatrix} = \begin{bmatrix} AE+BG&AF+BH \\ CE+DG&CF+DH \end{bmatrix}$

with the size of each element as follows:

$AE+BG$ is $m_1$ by $n_1$
$AF+BH$ is $m_1$ by $n_2$
$CE+DG$ is $m_2$ by $n_1$
$CF+DH$ is $m_2$ by $n_2$

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.13

Posted on February 10, 2013 by hecker

Exercise 2.5.13. Given a graph with 4 nodes and 6 edges, what are the spanning trees for the graph (16 in all)?

Answer: The graph has 4 nodes and 6 edges. Assume that the graph is as follows:

edge 1 from node 1 to node 2
edge 2 from node 2 to node 3
edge 3 from node 3 to node 4
edge 4 from node 4 to node 1
edge 5 from node 1 to node 3
edge 6 from node 2 to node 4

This graph is equivalent to a square and its two diagonals, with the first 4 edges (edges 1 through 4) forming the outside of the square and the last 2 edges (edges 5 and 6) forming the diagonals.

Since the graph has 4 nodes, all spanning trees contain 3 edges. The first four spanning trees correspond to the outside edges of the square with one edge removed:

edge 1, edge 2, edge 3
edge 2, edge 3, edge 4
edge 3, edge 4, edge 1
edge 4, edge 1, edge 2

The next four spanning trees include two adjacent outside edges of the square and one diagonal edge, with the diagonal edge connecting to the node between the two outside edges:

edge 1, edge 2, edge 6
edge 2, edge 3, edge 5
edge 3, edge 4, edge 6
edge 4, edge 1, edge 5

The next four spanning trees include two opposite outside edges of the square and one diagonal edge connecting the two sides:

edge 1, edge 3, edge 5
edge 1, edge 3, edge 6
edge 2, edge 4, edge 5
edge 2, edge 4, edge 6

The final four spanning trees include one outside edge of the square and the two diagonal edges:

edge 1, edge 5, edge 6
edge 2, edge 6, edge 5
edge 3, edge 5, edge 6
edge 4, edge 6, edge 5

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 2.5.12

Posted on February 3, 2013 by hecker

Exercise 2.5.12. Let $A$ be a 12 by 7 incidence matrix for a connected graph. What are the following values?

the rank of $A$
the number of free variables in the solution for the system $Ax = b$
the number of free variables in the solution for the system $A^Ty = f$
the number of edges that must be removed in order to convert the graph into a spanning tree

Answer: Each row in the incidence matrix $A$ corresponds to an edge of the graph and each column of $A$ corresponds to a node of the graph. Since $A$ is a 12 by 7 matrix the graph has 12 edges and 7 nodes. Since the graph is connected each node has at least one edge into or out of it.

Per the discussion on page 106, for a connected graph with 7 nodes all spanning trees contain 6 edges. (A example of such a spanning tree is a graph with an edge from node 1 to each of nodes 2 through 7.) We must therefore remove 6 of the 12 edges to form a spanning tree.

The rank of $A$ is 6, the number of edges in the spanning tree.

The system $Ax = b$ is a system of 12 equations in 7 unknowns. Since the rank of $A$ is 6 there are 6 pivots and 1 free variable in the solution.

The system $A^Ty = f$ is a system of 7 equations in 12 unknowns. Since the rank of $A^T$ is 6 (same as the rank of $A$ ) there are 6 pivots and 6 free variables in the solution.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | Leave a comment

My Math Homework

Linear Algebra and Its Applications, Exercise 2.6.2

Linear Algebra and Its Applications, Exercise 2.6.1

Linear Algebra and Its Applications, Exercise 2.5.19

Linear Algebra and Its Applications, Exercise 2.5.18

Linear Algebra and Its Applications, Exercise 2.5.17

Linear Algebra and Its Applications, Exercise 2.5.16

Linear Algebra and Its Applications, Exercise 2.5.15

Linear Algebra and Its Applications, Exercise 2.5.14

Linear Algebra and Its Applications, Exercise 2.5.13

Linear Algebra and Its Applications, Exercise 2.5.12

Archives

Meta