Exercise 2.4.3. For each of the two matrices below give the dimension and find a basis for each of their four subspaces:
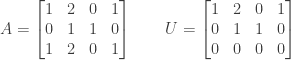
Answer: We first consider the column spaces  and
and 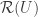 . The matrix
. The matrix  has two pivots and therefore rank
has two pivots and therefore rank 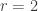 ; this is the dimension of the column space of
; this is the dimension of the column space of  . Since the pivots are in the first and second columns those columns are a basis for
. Since the pivots are in the first and second columns those columns are a basis for 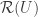 :
:

Note that the third column of  is equal to -2 times the first column plus the second column, and the fourth column is equal to the first column.
is equal to -2 times the first column plus the second column, and the fourth column is equal to the first column.
Doing Gaussian elimination on the matrix  (i.e., by subtracting the first row from the third) produces
(i.e., by subtracting the first row from the third) produces  , so the rank of
, so the rank of  and the dimension of the column space of
and the dimension of the column space of  are also 2. Also, since the first and second columns of
are also 2. Also, since the first and second columns of  (the pivot columns) are a basis for
(the pivot columns) are a basis for 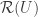 the first and second columns of
the first and second columns of  are a basis for
are a basis for  :
:

Note that as with  the third column of
the third column of  is equal to -2 times the first column plus the second column, and the fourth column is equal to the first column.
is equal to -2 times the first column plus the second column, and the fourth column is equal to the first column.
Turning to the row spaces, since the rows of  are linear combinations of the rows of
are linear combinations of the rows of  and vice versa, the row spaces
and vice versa, the row spaces  and
and 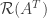 are the same. Per the discussion on page 91 the nonzero rows of
are the same. Per the discussion on page 91 the nonzero rows of  , the vectors
, the vectors 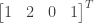 and
and  , form a basis for
, form a basis for  . Since
. Since 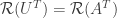 these vectors also form a basis for
these vectors also form a basis for 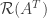 . The dimension of each row space is 2.
. The dimension of each row space is 2.
We now turn to the nullspaces  and
and  consisting of the solutions to the equations
consisting of the solutions to the equations 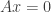 and
and 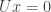 respectively. As noted above, if we do Gaussian elimination on
respectively. As noted above, if we do Gaussian elimination on  (i.e., by subtracting the first row from the third row) then we obtain the matrix
(i.e., by subtracting the first row from the third row) then we obtain the matrix  so that any solution to
so that any solution to 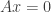 is a solution to
is a solution to 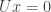 and vice versa. We therefore have
and vice versa. We therefore have 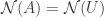 and just need to calculate one of the two.
and just need to calculate one of the two.
In particular for 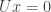 we must find
we must find  such that
such that

Since the pivots of  are in the first and second columns we have
are in the first and second columns we have 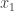 and
and  as basic variables and
as basic variables and 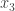 and
and 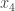 as free variables.
as free variables.
From the second row of the system above we have  or
or  . From the first row we then have
. From the first row we then have  or
or  . Setting each of the free variables
. Setting each of the free variables 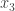 and
and 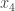 to 1 in turn (and the other free variable to zero) we have the following set of vectors as solutions to the homogeneous equation
to 1 in turn (and the other free variable to zero) we have the following set of vectors as solutions to the homogeneous equation 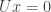 and a basis for the null space of
and a basis for the null space of  :
:

Since 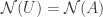 the above vectors also form a basis for the nullspace of
the above vectors also form a basis for the nullspace of  . The dimension of the two nullspaces
. The dimension of the two nullspaces  and
and  is 2 (the number of columns of each matrix minus the rank, or
is 2 (the number of columns of each matrix minus the rank, or  ).
).
Finally we turn to finding a basis for each of the left nullspaces  and
and  . As discussed on page 95 there are two possible approaches to doing this. One way to find the left nullspace of
. As discussed on page 95 there are two possible approaches to doing this. One way to find the left nullspace of  is to look at the operations on the rows of
is to look at the operations on the rows of  needed to produce zero rows in the resulting echelon matrix
needed to produce zero rows in the resulting echelon matrix  in the process of Gaussian elimination; the coefficients used to carry out those operations make up the basis vectors of the left nullspace
in the process of Gaussian elimination; the coefficients used to carry out those operations make up the basis vectors of the left nullspace  .
.
In particular, the one and only zero row in  is produced by subtracting the first row of
is produced by subtracting the first row of  from the third row of
from the third row of  , with no contribution from the second row; the coefficients for this operation are -1 (for the first row), 0 (for the second row), and 1 (for the third). The vector
, with no contribution from the second row; the coefficients for this operation are -1 (for the first row), 0 (for the second row), and 1 (for the third). The vector

is therefore a basis for the left nullspace  (which has dimension 1). We can test this by multiplying
(which has dimension 1). We can test this by multiplying  on the left by the transpose of this vector:
on the left by the transpose of this vector:

The left nullspace of  can be found in a similar manner: Since
can be found in a similar manner: Since  is already in echelon form with a third row of zeroes, the step of Gaussian elimination to produce that row would be equivalent to multiplying the first row by zero and the second row by zero and then adding them to the third (zero) row; the coefficients for this operation are 0 (for the first row), 0 (for the second row), and 1 (for the third row). The vector
is already in echelon form with a third row of zeroes, the step of Gaussian elimination to produce that row would be equivalent to multiplying the first row by zero and the second row by zero and then adding them to the third (zero) row; the coefficients for this operation are 0 (for the first row), 0 (for the second row), and 1 (for the third row). The vector
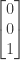
is therefore a basis for the left nullspace 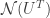 (which also has dimension 1). As with
(which also has dimension 1). As with  we can test this by multiplying
we can test this by multiplying  on the left by the transpose of this vector:
on the left by the transpose of this vector:

An alternate approach to find the left nullspace of  is to explicitly solve
is to explicitly solve  or
or

Gaussian elimination on  proceeds as follows: First, subtract two times the first row from the second:
proceeds as follows: First, subtract two times the first row from the second:

and then subtract the first row from the fourth row:

Finally, subtract the second row from the third row:
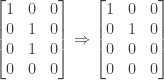
We thus have 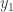 and
and 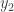 as basic variables (since the pivots are in the first and second columns) and
as basic variables (since the pivots are in the first and second columns) and  as a free variable. From the first row of the final matrix we have
as a free variable. From the first row of the final matrix we have  or
or  in the homogeneous case, and from the second row of the final matrix we have
in the homogeneous case, and from the second row of the final matrix we have  or
or 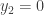 . Setting the free variable
. Setting the free variable  then gives us the vector
then gives us the vector
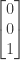
as a basis for the left nullspace of  . The left nullspace of
. The left nullspace of  has dimension 1 (the number of rows of
has dimension 1 (the number of rows of  minus its rank, or
minus its rank, or  ).
).
Similarly we can also find the left nullspace of  by solving the homogeneous system
by solving the homogeneous system 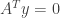 or
or
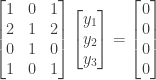
Gaussian elimination on  proceeds as follows: First, subtract two times the first row from the second:
proceeds as follows: First, subtract two times the first row from the second:

and then subtract the first row from the fourth row:
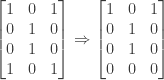
Finally, subtract the second row from the third row:

We thus have 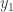 and
and 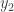 as basic variables (since the pivots are in the first and second columns) and
as basic variables (since the pivots are in the first and second columns) and  as a free variable. From the first row of the final matrix we have
as a free variable. From the first row of the final matrix we have  or
or  in the homogeneous case, and from the second row of the final matrix we have
in the homogeneous case, and from the second row of the final matrix we have  or
or 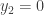 . Setting the free variable
. Setting the free variable  then gives us the vector
then gives us the vector

as a basis for the left nullspace of  . As with
. As with  the left nullspace of
the left nullspace of  has dimension 1 (the number of rows of
has dimension 1 (the number of rows of  minus its rank, or
minus its rank, or  ).
).
As with exercise 2.4.2, note that the row space of  is equal to the row space of
is equal to the row space of  because the rows of
because the rows of  are linear combinations of the rows of
are linear combinations of the rows of  and vice versa. Similarly the nullspace of
and vice versa. Similarly the nullspace of  is equal to the nullspace of
is equal to the nullspace of  for the same reason.
for the same reason.
UPDATE: Corrected two typos involving the equations for the left nullspace; thanks to Lucas for finding the errors.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
 Buy me a snack to sponsor more posts like this!
Buy me a snack to sponsor more posts like this!
the system
has at least one nonzero solution. Show that there exists at least one vector
for which the system
has no solution. Show an example of such a matrix
and vector
.
is an
by
matrix. If there exists a nonzero
for which
then the columns of
are linearly dependent. (If they were linearly independent then
would imply that
for all
.) We therefore have the rank
.
and the dimension of the row space
is equal to
the dimension of
is less than
. In other words, the rows of
do not span all of
.
in
that is not in
and cannot be expressed as a linear combination of the rows of
. Therefore for the vector
there is no solution to the system
. (If there were such a solution then its coefficients
would define a linear combination of the rows of
equal to
.)
is equivalent to
with
as a basic variable and
as a free variable.
or
. If we set the free variable
to 1 we then have
and
as a (nonzero) solution to
.
is a basis for the row space
, which consists of all vectors of the form
. Geometically this is a line through the origin and the point
.
, and consider the vector
and the system
while the second equation produces
, a contradiction. There is thus no solution to
for the example values of
and
.
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.

