Review exercise 2.26. State whether the following statements are true or false:
a) For every subspace  of
of 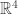 there exists a matrix
there exists a matrix  for which the nullspace of
for which the nullspace of  is
is  .
.
b) For any matrix  , if both
, if both  and its transpose
and its transpose  have the same nullspace then
have the same nullspace then  is a square matrix.
is a square matrix.
c) The transformation from 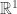 to
to 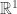 that transforms
that transforms  into
into 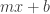 (for some scalars
(for some scalars  and
and  ) is a linear transformation.
) is a linear transformation.
Answer: a) For the statement to be true, for any subspace  of
of 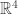 we must be able to find a matrix
we must be able to find a matrix  such that
such that  . (In other words, for any vector
. (In other words, for any vector  in
in  we have
we have 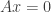 and for any
and for any  such that
such that 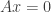 the vector
the vector  is an element of
is an element of  .)
.)
What would such a matrix  look like? First, since
look like? First, since  is a subspace of
is a subspace of 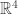 any vector
any vector  in
in  has four entries:
has four entries:  . If we have
. If we have 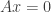 then the matrix
then the matrix  must have four columns; otherwise
must have four columns; otherwise  would not be able to multiply
would not be able to multiply  from the left side.
from the left side.
Second, note that the nullspace of  and the column space of
and the column space of  are related: If the column space has dimension
are related: If the column space has dimension  then the nullspace of
then the nullspace of  has dimension
has dimension 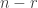 where
where  is the number of columns of
is the number of columns of  . Since
. Since  has four columns (from the previous paragraph) the dimension of
has four columns (from the previous paragraph) the dimension of  is
is  .
.
Put another way, if  is the dimension of
is the dimension of  and
and  is the nullspace of
is the nullspace of  then we must have
then we must have 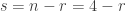 or
or 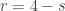 . So if the dimension of
. So if the dimension of  is
is 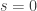 then we have
then we have  , if the dimension of
, if the dimension of  is
is 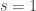 then we have
then we have 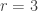 , and so on.
, and so on.
Finally, if the matrix  has rank
has rank  then
then  has both
has both  linearly independent columns and
linearly independent columns and  linearly independent rows. As noted above, the number of columns of
linearly independent rows. As noted above, the number of columns of  (linearly independent or otherwise) is fixed by the requirement that the nullspace of
(linearly independent or otherwise) is fixed by the requirement that the nullspace of  should be a subspace of
should be a subspace of 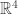 . So
. So  must always have four columns, and must have at least
must always have four columns, and must have at least 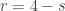 rows.
rows.
We now have five possible cases to consider, and can approach them as follows:
 has dimension 0 or 4. In both these cases there is only one possible subspace
has dimension 0 or 4. In both these cases there is only one possible subspace  and we can easily find a matrix
and we can easily find a matrix  meeting the specified criteria.
meeting the specified criteria. has dimension 1, 2, or 3. In each of these cases there are many possible subspaces
has dimension 1, 2, or 3. In each of these cases there are many possible subspaces  (an infinite number, in fact). For a given
(an infinite number, in fact). For a given  we do the following:
we do the following:
- Start with a basis for
 . (Any basis will do.)
. (Any basis will do.)
- Consider the effect on the basis vectors if they were to be in the nullspace of some matrix
 meeting the criteria above.
meeting the criteria above.
- Take the corresponding system of linear equations, re-express it as a system involving the entries of
 as unknowns and the entries of the basis vectors as coefficients, and show that we can solve the system to find the unknowns.
as unknowns and the entries of the basis vectors as coefficients, and show that we can solve the system to find the unknowns.
- Show that all other vectors in
 are also in the nullspace of
are also in the nullspace of  .
.
- Show that any vector in the nullspace of
 must also be in
must also be in  .
.
We now proceed to the individual cases:
 has dimension
has dimension  . We then have
. We then have  . (If
. (If  has dimension 4 then its basis has four linearly independent vectors. If
has dimension 4 then its basis has four linearly independent vectors. If 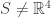 then there must be some vector
then there must be some vector  in
in 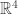 but not in
but not in  , and that vector must be linearly independent of the vectors in the basis of
, and that vector must be linearly independent of the vectors in the basis of  . But it is impossible to have five linearly independent vectors in a 4-dimensional vector space, so we conclude that
. But it is impossible to have five linearly independent vectors in a 4-dimensional vector space, so we conclude that  .)
.)
We then must have 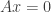 for any vector
for any vector  in
in  . This is true when
. This is true when  is equal to the zero matrix. As noted above
is equal to the zero matrix. As noted above  must have exactly four columns and at least
must have exactly four columns and at least  rows. So one possible value for
rows. So one possible value for  is
is

(The matrix  could have additional rows as well, as long as they are all zeros.)
could have additional rows as well, as long as they are all zeros.)
We have thus found a matrix  such that any vector
such that any vector  in
in  is also in
is also in  . Going the other way, any vector
. Going the other way, any vector  in
in  must have four entries (in order for
must have four entries (in order for  to be able to multiply it) so that any such vector
to be able to multiply it) so that any such vector  is also in
is also in  .
.
So if  is a 4-dimensional subspace (namely
is a 4-dimensional subspace (namely 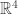 ) then a matrix
) then a matrix  exists such that
exists such that  is the nullspace of
is the nullspace of  .
.
 has dimension
has dimension 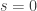 . The only 0-dimensional subspace of
. The only 0-dimensional subspace of 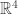 is that consisting only of the zero vector
is that consisting only of the zero vector  . (If
. (If  contained only a single nonzero vector then it would not be closed under multiplication, since multiplying that vector times the scalar 0 would produce a vector not in
contained only a single nonzero vector then it would not be closed under multiplication, since multiplying that vector times the scalar 0 would produce a vector not in  . If
. If  were not closed under multiplication then it would not be a subspace.)
were not closed under multiplication then it would not be a subspace.)
In this case the matrix  would have to have rank
would have to have rank  . If
. If 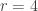 then all four columns of
then all four columns of  would have to be linearly independent and
would have to be linearly independent and  would have to have at least four linearly independent rows. Suppose we choose the four elementary vectors
would have to have at least four linearly independent rows. Suppose we choose the four elementary vectors 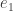 through
through  as the columns, so that
as the columns, so that

If 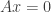 we then have
we then have

so that the only solution is  . We have thus again found a matrix
. We have thus again found a matrix  for which
for which  .
.
(Note that any other matrix of rank 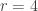 would have worked as well: The product
would have worked as well: The product 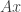 is a linear combination of the columns of
is a linear combination of the columns of  , with the coefficients being
, with the coefficients being 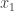 through
through 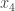 . If the columns of
. If the columns of  are linearly independent then that linear combination can be zero only if all the coefficients
are linearly independent then that linear combination can be zero only if all the coefficients 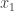 through
through 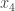 are zero.)
are zero.)
Having disposed of the easy cases, we now proceed to the harder ones.
 has dimension
has dimension 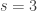 . In this case we are looking for a matrix
. In this case we are looking for a matrix  with rank
with rank 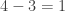 such that
such that  . The matrix
. The matrix  thus must have only one linearly independent column and (more important for our purposes) only one linearly independent row. We need only find a matrix that is 1 by 4. (If desired we can construct suitable matrices that are 2 by 4, 3 by 4, etc., by adding additional rows that are multiples of the first row.)
thus must have only one linearly independent column and (more important for our purposes) only one linearly independent row. We need only find a matrix that is 1 by 4. (If desired we can construct suitable matrices that are 2 by 4, 3 by 4, etc., by adding additional rows that are multiples of the first row.)
Since the dimension of  is 3, any three linearly independent vectors in
is 3, any three linearly independent vectors in  form a basis for
form a basis for  ; we pick an arbitrary set of such vectors
; we pick an arbitrary set of such vectors  ,
,  , and
, and  . For
. For  to be equal to
to be equal to  we must have
we must have  ,
,  , and
, and  . We are looking for a matrix
. We are looking for a matrix  that is 1 by 4, so these equations correspond to the following:
that is 1 by 4, so these equations correspond to the following:

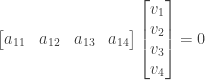
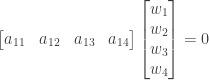
These can in turn be rewritten as the following system of equations:

This is a system of three equations in four unknowns, equivalent to the matrix equation  where
where
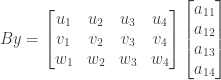
Since the vectors  ,
,  , and
, and  are linearly independent (because they form a basis for the 3-dimensional subspace
are linearly independent (because they form a basis for the 3-dimensional subspace  ) and the vectors in question form the rows of the matrix
) and the vectors in question form the rows of the matrix  , the rank of
, the rank of  is
is 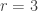 . We also have
. We also have  , the number of rows of
, the number of rows of  . Since this is true, per 20Q on page 96 there exists at least one solution
. Since this is true, per 20Q on page 96 there exists at least one solution  to the above system
to the above system  . But
. But  is simply the first and only row in the matrix we were looking for, so this in turn means that we have found a matrix
is simply the first and only row in the matrix we were looking for, so this in turn means that we have found a matrix  for which
for which  ,
,  , and
, and  are in the nullspace of
are in the nullspace of  .
.
If  is a vector in
is a vector in  then
then  can be expressed as a linear combination of the basis vectors
can be expressed as a linear combination of the basis vectors  ,
,  , and
, and  for some set of coefficients
for some set of coefficients 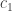 ,
, 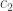 , and
, and 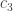 . We then have
. We then have



So any vector  in
in  is also an element in the nullspace of
is also an element in the nullspace of  .
.
Suppose that  is a vector in the nullspace of
is a vector in the nullspace of  and
and  is not in
is not in  . Since
. Since  is not in
is not in  it cannot be expressed as a linear combination solely of the basis vectors
it cannot be expressed as a linear combination solely of the basis vectors  ,
,  , and
, and  ; rather we must have
; rather we must have

where  is some vector that is linearly independent of
is some vector that is linearly independent of  ,
,  , and
, and  .
.
If  is in the nullspace of
is in the nullspace of  then we have
then we have 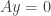 so
so


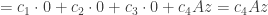
If  then either
then either 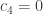 or
or  . If
. If 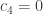 then we have
then we have

so that  is actually an element of
is actually an element of  , contrary to our supposition. If
, contrary to our supposition. If  then
then  is an element of the nullspace of
is an element of the nullspace of  . But
. But  has dimension 3 and already contains the three linearly independent vectors
has dimension 3 and already contains the three linearly independent vectors  ,
,  , and
, and  . The fourth vector
. The fourth vector  cannot be both an element of
cannot be both an element of  and also linearly independent of
and also linearly independent of  ,
,  , and
, and  .
.
Our assumption that  is in the nullspace of
is in the nullspace of  but is not in
but is not in  has thus led to a contradiction. We conclude that any element of
has thus led to a contradiction. We conclude that any element of  is also in
is also in  . We previously showed that any element of
. We previously showed that any element of  is also in
is also in  , so we conclude that
, so we conclude that  .
.
For any 3-dimensional subspace  of
of 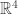 we can therefore find a matrix
we can therefore find a matrix  such that
such that  is the nullspace of
is the nullspace of  .
.
 has dimension
has dimension  . In this case we are looking for a matrix
. In this case we are looking for a matrix  with rank
with rank  such that
such that  . The matrix
. The matrix  thus must have only two linearly independent columns and only two linearly independent rows. We thus look for a matrix that is 2 by 4.
thus must have only two linearly independent columns and only two linearly independent rows. We thus look for a matrix that is 2 by 4.
Since the dimension of  is 2, any two linearly independent vectors in
is 2, any two linearly independent vectors in  form a basis for
form a basis for  ; we pick an arbitrary set of such vectors
; we pick an arbitrary set of such vectors  and
and  . For
. For  to be equal to
to be equal to  we must have
we must have  and
and  . We are looking for a matrix
. We are looking for a matrix  that is 2 by 4, so these equations correspond to the following:
that is 2 by 4, so these equations correspond to the following:
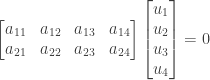

These can in turn be rewritten as the following system of four equations in eight unknowns:
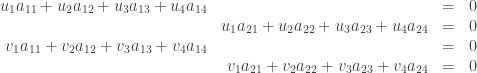
or  where
where
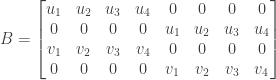
Since the four rows are linearly independent (this follows from the linear independence of  and
and  ) we have
) we have  so that the system is guaranteed to have a solution
so that the system is guaranteed to have a solution  . The entries in
. The entries in  are just the entries of
are just the entries of  so we have found a matrix
so we have found a matrix  for which the basis vectors
for which the basis vectors  and
and  are members of the nullspace.
are members of the nullspace.
Since the basis vectors of  are in
are in  all other elements of
all other elements of  are in
are in  also. By the same argument as in the 3-dimensional case, any vector
also. By the same argument as in the 3-dimensional case, any vector  in
in  must be in
must be in  also; otherwise a contradiction occurs. Thus we conclude that
also; otherwise a contradiction occurs. Thus we conclude that  .
.
For any 2-dimensional subspace  of
of  we can therefore find a matrix
we can therefore find a matrix  such that
such that  is the nullspace of
is the nullspace of  .
.
 has dimension
has dimension  . In this case we are looking for a matrix
. In this case we are looking for a matrix  with rank
with rank  such that
such that  . The matrix
. The matrix  thus must have only three linearly independent columns and only three linearly independent rows. We thus look for a matrix that is 3 by 4.
thus must have only three linearly independent columns and only three linearly independent rows. We thus look for a matrix that is 3 by 4.
Since the dimension of  is 1, any nonzero vector
is 1, any nonzero vector  in
in  forms a basis for
forms a basis for  . For
. For  to be equal to
to be equal to  we must have
we must have  . We are looking for a matrix
. We are looking for a matrix  that is 3 by 4, so this equation corresponds to the following:
that is 3 by 4, so this equation corresponds to the following:

This can be rewritten as a system  of three equations with twelve unknowns (
of three equations with twelve unknowns ( ), a system which is guaranteed to have at least one solution due to the linear independence of the three rows of
), a system which is guaranteed to have at least one solution due to the linear independence of the three rows of  . The solution then forms the entries of
. The solution then forms the entries of  , so that we have
, so that we have  . Since
. Since  is a basis for
is a basis for  any other vector in
any other vector in  is also in the nullspace of
is also in the nullspace of  .
.
By the same argument as in the 3-dimensional case, any vector  in
in  must be in
must be in  also; otherwise a contradiction occurs. Thus we conclude that
also; otherwise a contradiction occurs. Thus we conclude that  .
.
For any 1-dimensional subspace  of
of  we can therefore find a matrix
we can therefore find a matrix  such that
such that  is the nullspace of
is the nullspace of  .
.
Any subspace of 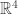 must have dimension from 0 through 4. We have thus shown that for any subspace
must have dimension from 0 through 4. We have thus shown that for any subspace  of
of 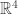 we can find a matrix
we can find a matrix  such that
such that  . The statement is true.
. The statement is true.
b) Suppose that for some  by
by  matrix
matrix  both
both  and its transpose
and its transpose  have the same nullspace.
have the same nullspace.
The rank  of
of  is also the rank of
is also the rank of  . The rank of
. The rank of  is then
is then 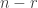 , and the rank of
, and the rank of  is
is 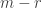 . Since
. Since  we then have
we then have  so that
so that 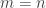 .
.
The number of rows  of
of  is the same as the number of columns
is the same as the number of columns  of
of  so that
so that  (and thus
(and thus  ) is a square matrix. The statement is true.
) is a square matrix. The statement is true.
c) If 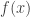 represents the transformation in question, with
represents the transformation in question, with  , we have
, we have


These two quantities are not the same unless 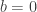 , so for
, so for 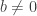 the transformation is not linear. The statement is false.
the transformation is not linear. The statement is false.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
 Buy me a snack to sponsor more posts like this!
Buy me a snack to sponsor more posts like this!
and
what is the length of each vector and their inner product?
and
.
and
is then
and
are thus orthogonal.
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.

