Exercise 2.1.7. Of the following, which are subspaces of 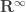 ?
?
(a) the set of all sequences that include infinitely many zeros, e.g., 
(b) the set of all sequences of the form  where
where  from some point onward
from some point onward
(c) the set of all decreasing sequences, i.e.,  for all
for all 
(d) the set of all sequences such that 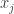 converges to a limit as
converges to a limit as 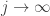
(e) the set of all arithmetic progressions for which 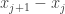 is constant for all
is constant for all 
(f) the set of all geometric progressions of the form  for any choice of
for any choice of 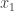 and
and 
Answer: (a) This set is not a subspace because it is not closed under addition: If we have  and
and  then both
then both  and
and  are in the set but their sum
are in the set but their sum  is not.
is not.
(b) This set is closed under scalar multiplication: Consider  and suppose for some
and suppose for some  we have
we have  for
for 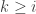 . We then have
. We then have 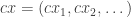 . Since we have
. Since we have  for
for 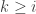 we also have
we also have  for
for 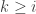 . So
. So  is also a member of the set.
is also a member of the set.
This set is also closed under vector addition. Consider  from above and
from above and  where
where 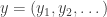 and for some
and for some  we have
we have 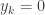 for
for 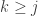 , and consider the sum
, and consider the sum 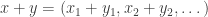 . Choose
. Choose  so that
so that  and
and  . Then
. Then  for
for  and
and 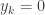 for
for  so that
so that  for
for  . The sum
. The sum 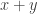 is therefore also a member of the set.
is therefore also a member of the set.
Since the set is closed under both vector addition and scalar multiplication and it is a subset of the vector space of infinite sequences, it is a subspace of that vector space.
(c) This set is not a subspace because it is not closed under scalar multiplication: The sequence 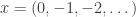 is a member of the set, but
is a member of the set, but 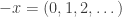 is not.
is not.
(d) We first check that the set of converging sequences is closed under scalar multiplication. Let  be a member of this set, so that
be a member of this set, so that  exists. Then for any
exists. Then for any 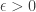 there exists
there exists  such that
such that  for
for 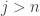 . Now consider
. Now consider  where
where  is any scalar. If
is any scalar. If  then
then 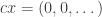 so that it converges to the limit 0.
so that it converges to the limit 0.
Suppose that  and choose any
and choose any 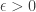 . Since
. Since  exists we can choose
exists we can choose  such that
such that  for
for 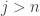 . Multiplying both sides by
. Multiplying both sides by 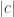 we have
we have  . But
. But  . We therefore see that for any
. We therefore see that for any 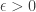 we can choose
we can choose  such that
such that  .
.
This means that  exists and is equal to
exists and is equal to 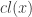 so that for any scalar
so that for any scalar  and converging sequence
and converging sequence  the sequence
the sequence  is also in the set of converging sequences. Since
is also in the set of converging sequences. Since  converges both for
converges both for  and
and  the set is therefore closed under scalar multiplication.
the set is therefore closed under scalar multiplication.
We next check that the set of converging sequences is closed under vector addition. Let  also be a member of this set, so that
also be a member of this set, so that 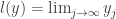 exists. Then for any
exists. Then for any 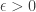 there exists
there exists  such that
such that  for
for 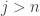 .
.
Now consider  and choose any
and choose any 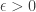 . Since
. Since  exists we can choose
exists we can choose  such that
such that  for
for 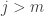 , and since
, and since  exists we can choose
exists we can choose  such that
such that 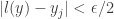 for
for 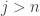 . Choose
. Choose  such that
such that  and
and  . Adding both sides of the two inequalities we have
. Adding both sides of the two inequalities we have  for
for 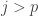 .
.
We have  for any
for any  and
and  , and thus for any
, and thus for any 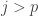 we have
we have

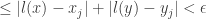
So for any 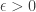 we can choose
we can choose  such that
such that  for all
for all 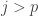 . This means that
. This means that  exists and is equal to
exists and is equal to  so that for any two converging sequences
so that for any two converging sequences  and
and  the sequence
the sequence 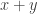 is also in the set of converging sequences. The set is therefore closed under vector addition.
is also in the set of converging sequences. The set is therefore closed under vector addition.
Since the set of converging sequences is closed under both vector addition and scalar multiplication and it is a subset of the vector space of infinite sequences, it is a subspace of that vector space.
(e) We first check that the set of arithmetic progressions is closed under scalar multiplication. Let  be a member of this set, so that
be a member of this set, so that 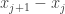 is a constant value
is a constant value  for all
for all  . Then for
. Then for  we have
we have  for all
for all  . The sequence
. The sequence  is therefore also an arithmetic progression, and the set is closed under scalar multiplication.
is therefore also an arithmetic progression, and the set is closed under scalar multiplication.
We next check that the set of arithmetic progressions is closed under vector addition. Let  also be a member of this set, so that
also be a member of this set, so that 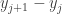 is a constant value
is a constant value  for all
for all  . Then for
. Then for  we have
we have

for all  . The sequence
. The sequence 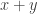 is therefore also an arithmetic progression, and the set is closed under vector addition.
is therefore also an arithmetic progression, and the set is closed under vector addition.
Since the set of arithmetic progressions is closed under both vector addition and scalar multiplication and it is a subset of the vector space of infinite sequences, it is a subspace of that vector space.
(f) The set of geometric progressions is not a subspace because it is not closed under vector addition: For example, suppose that 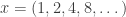 (for which
(for which  and
and  ), and
), and  (for which
(for which  and
and  ). We then have
). We then have  . For
. For 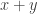 we have
we have 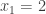 (from the first element) and
(from the first element) and  (from the second element). If
(from the second element). If 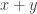 is a geometric progression then the third element should be
is a geometric progression then the third element should be  instead of the actual value of 13. So
instead of the actual value of 13. So 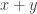 is not a geometrical progression for all geometric progressions
is not a geometrical progression for all geometric progressions  and
and  , and the set is not closed under vector addition.
, and the set is not closed under vector addition.
UPDATE: Fixed typos in the question ( should have been
should have been  ) and in the answers to (b) (
) and in the answers to (b) ( should have been
should have been  ) and (d) (
) and (d) ( should have been
should have been 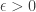 ).
).
UPDATE 2: Fixed typos in the question and answer for (f) (references to  and
and 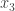 should have been to
should have been to 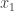 , and a reference to
, and a reference to 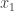 should have been to
should have been to 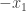 ).
).
UPDATE 3: Fixed the answer for (f); the original answer (claiming that 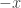 was not a geometric progression) was incorrect. Thanks go to Samuel for pointing this out.
was not a geometric progression) was incorrect. Thanks go to Samuel for pointing this out.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
form a point, line, or plane? Is it a subspace? Is it the nullspace of
? The column space of
?
corresponds to
and we can substitute into the first equation to obtain
or
. We therefore have
so that the set of solutions
can be represented as
is a free variable. The set of solutions
is therefore a line passing through the origin and the point
.
is the set of all vectors for which
it is by definition the nullspace
of
(see page 68).
is the set of all vectors
that are linear combinations of the columns of
:
are 3 by 1 vectors; the set of solutions
is not the same as the column space of
.
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.

