Review exercise 1.27. State whether the following are true or false. If true explain why, and if false provide a counterexample.
(1) If a matrix  can be factored as
can be factored as 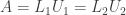 where
where 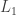 and
and 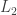 are lower triangular with unit diagonals and
are lower triangular with unit diagonals and 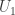 and
and 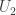 are upper triangular, then
are upper triangular, then  and
and  . (In other words, the factorization
. (In other words, the factorization  is unique.)
is unique.)
(2) If for a matrix  we have
we have 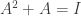 then
then  is invertible and
is invertible and  .
.
(3) If all the diagonal entries of a matrix  are zero then
are zero then  is singular.
is singular.
Answer: (1) True. Since 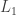 and
and 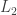 are lower triangular with unit diagonal both matrices are invertible, and their inverses are also lower triangular with unit diagonal. (See the proof of this below at the end of the post.) Similarly since
are lower triangular with unit diagonal both matrices are invertible, and their inverses are also lower triangular with unit diagonal. (See the proof of this below at the end of the post.) Similarly since 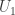 and
and 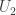 are upper triangular with nonzero diagonal those matrices are invertible as well, and their inverses are also upper triangular with nonzero diagonal.
are upper triangular with nonzero diagonal those matrices are invertible as well, and their inverses are also upper triangular with nonzero diagonal.
We then start with the equation  and multiply both sides by
and multiply both sides by  on the left and by
on the left and by  on the right:
on the right:

This equation reduces to  where
where  is the product matrix. Now since
is the product matrix. Now since  is the product of two lower triangular matrices with unit diagonal (i.e.,
is the product of two lower triangular matrices with unit diagonal (i.e.,  and
and 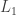 ), it itself is a lower triangular matrix with unit diagonal. Since
), it itself is a lower triangular matrix with unit diagonal. Since  is the product of two upper triangular matrices (i.e.,
is the product of two upper triangular matrices (i.e., 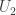 and
and  ), it is also an upper triangular matrix. Since
), it is also an upper triangular matrix. Since  is both lower triangular and upper triangular it must be a diagonal matrix, and since its diagonal entries are all 1 we must have
is both lower triangular and upper triangular it must be a diagonal matrix, and since its diagonal entries are all 1 we must have 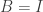 .
.
Since 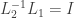 we can multiply both sides on the left by
we can multiply both sides on the left by 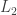 to obtain
to obtain 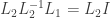 or
or  . Similarly since
. Similarly since  we can multiply both sides on the right by
we can multiply both sides on the right by 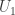 to obtain
to obtain  or
or  . So the factorization
. So the factorization  is unique.
is unique.
(2) True. Assume 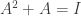 . We have
. We have 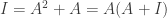 so that
so that  is a right inverse for
is a right inverse for  . We also have
. We also have 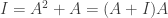 so that
so that 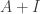 is a left inverse for
is a left inverse for  . Since
. Since 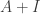 is both a left and right inverse of
is both a left and right inverse of  we know that
we know that  is invertible and that
is invertible and that  .
.
(3) False. The matrix
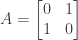
has zeros on the diagonal but is nonsingular. In fact we have

Proof of the result used in (1) above: Assume  is a lower triangular matrix with unit diagonal. That
is a lower triangular matrix with unit diagonal. That  is invertible can be seen from Gauss-Jordan elimination (here shown in a 4 by 4 example, although the argument generalizes to all
is invertible can be seen from Gauss-Jordan elimination (here shown in a 4 by 4 example, although the argument generalizes to all 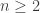 ):
):

Note that in forward elimination each of the diagonal entries of  will remain as is, since each of these entries has only zeros above it; each of the zero entries above the diagonal will remain unchanged as well, for the same reason. When forward elimination completes the left hand matrix will be the identity matrix since it will have zeros below the diagonal (from forward elimination), ones on the diagonal (as noted above), and zeroes above the diagonal (also as noted above). Gauss-Jordan elimination is thus guaranteed to complete successfully, so
will remain as is, since each of these entries has only zeros above it; each of the zero entries above the diagonal will remain unchanged as well, for the same reason. When forward elimination completes the left hand matrix will be the identity matrix since it will have zeros below the diagonal (from forward elimination), ones on the diagonal (as noted above), and zeroes above the diagonal (also as noted above). Gauss-Jordan elimination is thus guaranteed to complete successfully, so  is invertible.
is invertible.
The right-hand matrix at the end of Gauss-Jordan elimination will be the inverse of  . That matrix was produced from the identity matrix by forward elimination only, since backward elimination was not necessary. For the same reason noted above for the left-hand matrix, forward elimination will preserve the unit diagonal in the right-hand matrix and the zeros above it, with the only possible non-zero entries occurring below the unit diagonal. We thus see that if
. That matrix was produced from the identity matrix by forward elimination only, since backward elimination was not necessary. For the same reason noted above for the left-hand matrix, forward elimination will preserve the unit diagonal in the right-hand matrix and the zeros above it, with the only possible non-zero entries occurring below the unit diagonal. We thus see that if  is a lower-triangular matrix with unit diagonal then it is invertible and its inverse
is a lower-triangular matrix with unit diagonal then it is invertible and its inverse  is also a lower-triangular matrix with unit diagonal.
is also a lower-triangular matrix with unit diagonal.
Assume  is an upper triangular matrix with nonzero diagonal. That
is an upper triangular matrix with nonzero diagonal. That  is invertible can be seen from Gauss-Jordan elimination (again shown in a 4 by 4 example):
is invertible can be seen from Gauss-Jordan elimination (again shown in a 4 by 4 example):

Note that forward elimination is not necessary: There are nonzero entries on the diagonal and zeros below them, so we have pivots in every column; therefore the left-hand matrix  is nonsingular and is guaranteed to have an inverse.
is nonsingular and is guaranteed to have an inverse.
We can find that inverse by doing backward elimination to eliminate the entries above the diagonal in the left-hand matrix, and then dividing by the pivots. Note that since backward elimination starts with all zero entries below the diagonal in the right-hand matrix, it will not produce any nonzero entries below the diagonal in that matrix. Also, the diagonal entries in the right-hand matrix are not affected by backward elimination, for the same reason. After backward elimination completes the diagonal entries in the right-hand matrix will still be ones, and any nonzero entries produced will be above the diagonal. Dividing by the pivots in the left-hand matrix will then produce nonzero entries in the diagonal of the right-hand matrix.
The final right-hand matrix after completion of Gauss-Jordan elimination will therefore be an upper triangular matrix with nonzero diagonal entries. We thus see that if  is an upper-triangular matrix with nonzero diagonal then it is invertible and its inverse
is an upper-triangular matrix with nonzero diagonal then it is invertible and its inverse  is also an upper-triangular matrix with nonzero diagonal.
is also an upper-triangular matrix with nonzero diagonal.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
, and try to prove it by induction. Assume that for some
we have
we have
we have
and
, and we might guess that it holds true for
as well. We can test this as follows:
and subtracting it from the second row:
and subtract it from the third row:
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.

