Review exercise 1.12. State whether the following are true or false. If a statement is true explain why it is true. If a statement is false provide a counter-example.
(a) If  is invertible and
is invertible and  has the same rows as
has the same rows as  but in reverse order, then
but in reverse order, then  is invertible as well.
is invertible as well.
(b) If  and
and  are both symmetric matrices then their product
are both symmetric matrices then their product 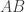 is also a symmetric matrix.
is also a symmetric matrix.
(c) If  and
and  are both invertible then their product
are both invertible then their product 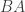 is also invertible.
is also invertible.
(d) If  is a nonsingular matrix then it can be factored into the product
is a nonsingular matrix then it can be factored into the product  of a lower triangular and upper triangular matrix.
of a lower triangular and upper triangular matrix.
Answer: (a) True. If  has the same rows as
has the same rows as  but in reverse order then we have
but in reverse order then we have 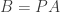 where
where 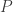 is the permutation matrix that reverses the order of rows. For example, for the 3 by 3 case we have
is the permutation matrix that reverses the order of rows. For example, for the 3 by 3 case we have

If we apply 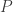 twice then it restores the order of the rows back to the original order; in other words
twice then it restores the order of the rows back to the original order; in other words  so that
so that 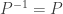 .
.
If  is invertible then
is invertible then 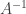 exists. Consider the product
exists. Consider the product  . We have
. We have

so that  is a right inverse for
is a right inverse for  . We also have
. We also have
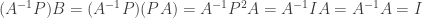
so that  is a left inverse for
is a left inverse for  as well. Since
as well. Since  is both a left and right inverse for
is both a left and right inverse for  we have
we have  so that
so that  is invertible if
is invertible if  is.
is.
Incidentally, note that while multiplying by 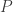 on the left reverses the order of the rows, multiplying by
on the left reverses the order of the rows, multiplying by 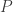 on the right reverse the order of the columns. For example, in the 3 by 3 case we have
on the right reverse the order of the columns. For example, in the 3 by 3 case we have

Thus if 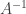 exists and
exists and 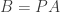 then
then  exists and consists of
exists and consists of 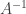 with its columns reversed.
with its columns reversed.
(b) False. The product of two symmetric matrices is not necessarily itself a symmetric matrix, as shown by the following counterexample:

(c) True. Suppose that both  and
and  are invertible; then both
are invertible; then both 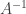 and
and 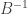 exist. Consider the product matrices
exist. Consider the product matrices 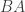 and
and  . We have
. We have
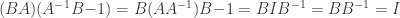
and also

So  is both a left and right inverse for
is both a left and right inverse for 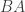 and thus
and thus 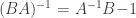 . If both
. If both  and
and  are invertible then their product
are invertible then their product 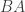 is also.
is also.
(d) False. A matrix  cannot necessarily be factored into the form
cannot necessarily be factored into the form  because you may need to do row exchanges in order for elimination to succeed. Consider the following counterexample:
because you may need to do row exchanges in order for elimination to succeed. Consider the following counterexample:
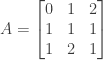
This matrix requires exchanging the first and second rows before elimination can commence. We can do this by multiplying by an appropriate permutation matrix:

We then multiply the (new) first row by 1 and subtract it from the third row (i.e., the multiplier  ):
):

and then multiply the second row by 1 and subtract it from the third ( ):
):
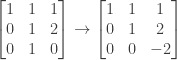
We then have

and

So a matrix  cannot always be factored into the form
cannot always be factored into the form  .
.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
into the form
(if
).
exists and has the same form as
.
times the second row from the third row (
) and subtracting
times the second row from the fourth row (
) :
times the second row and subtracting it from the first:
:
having the same form as
.
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.