Exercise 1.7.10. When partial pivoting is used show that 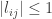 for all multipliers
for all multipliers  in
in 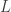 . In addition, show that if
. In addition, show that if 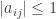 for all
for all 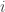 and
and 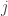 then after producing zeros in the first column we have
then after producing zeros in the first column we have  , and in general we have
, and in general we have  after producing zeros in column
after producing zeros in column 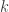 . Finally, show an 3 by 3 matrix with
. Finally, show an 3 by 3 matrix with 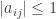 and
and 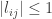 for which the last pivot is 4.
for which the last pivot is 4.
Answer: (a) With partial pivoting we choose the pivot 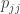 for each row and column in turn so that the pivot is the largest (in absolute value) of all the candidate pivots in the same column. Thus
for each row and column in turn so that the pivot is the largest (in absolute value) of all the candidate pivots in the same column. Thus  where
where 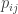 are all the other candidate pivots. The multipliers
are all the other candidate pivots. The multipliers  are then equal to the candidate pivots divided by the chosen pivot, so that
are then equal to the candidate pivots divided by the chosen pivot, so that 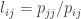 . But since
. But since  we have
we have  .
.
(b) Assume that 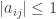 for all
for all 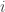 and
and 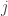 . Without loss of generality assume that
. Without loss of generality assume that  for all
for all 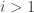 . (If this were not true then we could simply employ partial pivoting and do a row exchange to ensure that this would be the case.) Also assume that
. (If this were not true then we could simply employ partial pivoting and do a row exchange to ensure that this would be the case.) Also assume that 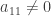 (i.e., the matrix is not singular). We then have
(i.e., the matrix is not singular). We then have  for
for 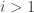 and thus
and thus 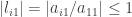 for
for 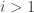 .
.
Let 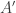 be the matrix produced after the first stage of elimination. Then for
be the matrix produced after the first stage of elimination. Then for 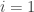 we have
we have  and thus
and thus  and thus
and thus 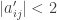 . For
. For 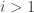 we have
we have 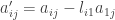 so that
so that  for
for 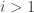 . But we have
. But we have 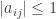 for all
for all 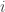 (and thus
(and thus 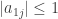 ) and
) and  for
for 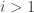 . Thus for the product
. Thus for the product  we have
we have  for
for 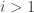 and for the difference
and for the difference  we have
we have  for
for 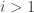 (with the maximum difference occurring when
(with the maximum difference occurring when 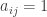 and
and  or vice versa).
or vice versa).
So we have 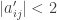 for
for 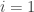 and we also have
and we also have  for
for 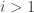 . For the matrix
. For the matrix 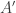 after the first stage of elimination we therefore have
after the first stage of elimination we therefore have  for all
for all 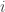 and
and 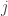 .
.
Assume that after stage 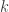 of elimination we have produced the matrix
of elimination we have produced the matrix 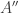 with
with 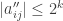 for all
for all 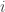 and
and 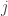 and consider stage
and consider stage 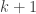 of elimination. In this stage our goal is to find an appropriate pivot for column
of elimination. In this stage our goal is to find an appropriate pivot for column 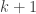 and produce zeros in column
and produce zeros in column 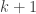 for all rows below
for all rows below 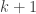 . Without loss of generality assume that
. Without loss of generality assume that  for all
for all 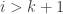 (otherwise we can do a row exchange as noted above). Also assume that
(otherwise we can do a row exchange as noted above). Also assume that 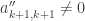 (i.e., the matrix is not singular). We then have
(i.e., the matrix is not singular). We then have  for
for 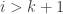 and thus
and thus  for
for 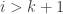 .
.
Let  be the matrix produced after stage
be the matrix produced after stage 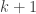 of elimination. Then for
of elimination. Then for 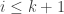 we have
we have  and thus
and thus  and thus
and thus  . For
. For 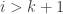 we have
we have 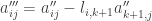 so that
so that  for
for 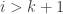 . But we have
. But we have 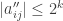 for all
for all 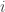 (and thus
(and thus  ) and
) and  for
for 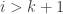 . Thus for the product
. Thus for the product 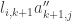 we have
we have 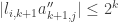 for
for 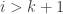 and for the difference
and for the difference  we have
we have 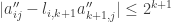 for
for 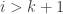 (with the maximum difference occurring when
(with the maximum difference occurring when  and
and  or vice versa).
or vice versa).
So we have  for
for 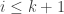 and we also have
and we also have  for
for 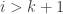 . For the matrix
. For the matrix  after stage
after stage 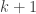 of elimination (which produces zeros in column
of elimination (which produces zeros in column 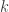 ) we therefore have
) we therefore have  for all
for all 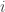 and
and 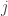 . For
. For 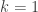 we also have
we also have  for all
for all 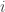 and
and 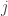 after the first stage of elimination (which produces zeros in column 1). Therefore by induction if in the original matrix
after the first stage of elimination (which produces zeros in column 1). Therefore by induction if in the original matrix  we have
we have 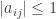 then for all
then for all 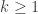 if we do elimination with partial pivoting then after stage
if we do elimination with partial pivoting then after stage 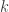 of elimination (which produces zeros in column
of elimination (which produces zeros in column 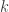 ) we will have a matrix
) we will have a matrix 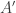 for which
for which 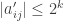 .
.
(c) One way to construct the requested matrix is to start with the desired end result and work backward to find a matrix for which elimination will produce that result, assuming that the absolute value of the multiplier at each step is 1 (the largest absolute value allowed under our assumption) and that after stage 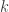 we have no value larger in absolute value than
we have no value larger in absolute value than 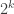 .
.
Thus in the final matrix (after stage 2 of elimination) we assume we have a pivot of 4 in column 3 but as yet unknown values for the other entries. The successive matrices at the various stages of elimination (the original matrix and the matrices after stage 1 and stage 2) would then be as follows:

We assume a multiplier of  for the single elimination step in stage 2, and prior to that step (i.e., after stage 1 of elimination) we can have no entry larger in absolute value than 2. The successive matrices at the various stages of elimination would then be as follows:
for the single elimination step in stage 2, and prior to that step (i.e., after stage 1 of elimination) we can have no entry larger in absolute value than 2. The successive matrices at the various stages of elimination would then be as follows:

so that subtracting row 2 from row 3 in stage 2 (i.e., using the multiplier  ) would produce the value 4 in the pivot position.
) would produce the value 4 in the pivot position.
We now need to figure out how to produce a value of 2 in the  position and a value of -2 in the
position and a value of -2 in the 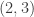 position after stage 1 of elimination. Stage 1 consists of two elimination steps, and we assume a multiplier of 1 or -1 for each step; also, all entries in the original matrix can have an absolute value no greater than 1. The original matrix prior to stage 1 of elimination can then be as follows:
position after stage 1 of elimination. Stage 1 consists of two elimination steps, and we assume a multiplier of 1 or -1 for each step; also, all entries in the original matrix can have an absolute value no greater than 1. The original matrix prior to stage 1 of elimination can then be as follows:

with the multiplier  and the multiplier
and the multiplier  (i.e., in stage 1 of elimination we are adding row 1 to row 2 and subtracting row 1 from row 3).
(i.e., in stage 1 of elimination we are adding row 1 to row 2 and subtracting row 1 from row 3).
Now that we have picked entries for column 3 in the original matrix and suitable multipliers for all elimination steps, we need to pick entries for column 1 and column 2 of the original matrix that are consistent with the chosen multipliers and ensure that elimination will produce nonzero pivots in columns 1 and 2.
We first pick values for the  and
and 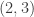 entries in the matrix after stage 1 of elimination; since we are using the multiplier
entries in the matrix after stage 1 of elimination; since we are using the multiplier  those entries should be the same in order to produce a zero in the
those entries should be the same in order to produce a zero in the 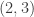 position after stage 2. We’ll try picking a value of 1 for both entries:
position after stage 2. We’ll try picking a value of 1 for both entries:

From above we know that in stage 1 of elimination row 1 is added to row 2 (i.e., the multiplier  ) and row 1 is subtracted from row 3 (i.e., the multiplier
) and row 1 is subtracted from row 3 (i.e., the multiplier  ). Since we have to end up with the same value in the
). Since we have to end up with the same value in the  and
and 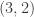 positions in either case, the easiest approach is to assume that the
positions in either case, the easiest approach is to assume that the 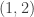 position in the original matrix has a zero entry, so that adding or subtracting it doesn’t change the preexisting entries for rows 2 and 3:
position in the original matrix has a zero entry, so that adding or subtracting it doesn’t change the preexisting entries for rows 2 and 3:
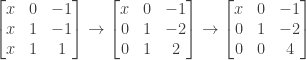
Finally, we need entries in the first column such that adding row 1 to row 2 and subtracting row 1 from row 3 will produce zero:

This completes our task. We now have a matrix

for which 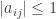 and
and 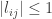 , and for which elimination produces a final pivot of 4.
, and for which elimination produces a final pivot of 4.
NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.
by Gilbert Strang.
If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition , Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books
and the accompanying free online course, and Dr Strang’s other books .
.
how are the rows of
related to the rows of
?
, the product
is a 3 by 3 matrix in which:
.
multiplied by 2.
and the third row of
.
, the product matrix
is a 2 by 3 matrix in which:
.
is a permutation matrix that reverses the order of rows, so that in the product
:
.
.
.
by Gilbert Strang.
, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition
and the accompanying free online course, and Dr Strang’s other books
.