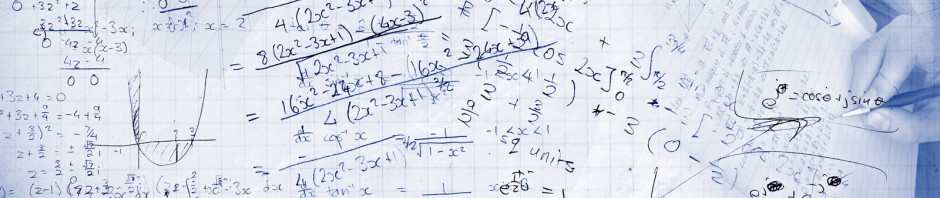Linear Algebra and Its Applications, Exercise 1.5.9

Posted on January 10, 2011 by hecker

Exercise 1.5.9. (a) Assume that A is the product of three matrices as follows:

A = \begin{bmatrix} 1&0&0 \\ -1&1&0 \\ 0&-1&1 \end{bmatrix} \begin{bmatrix} d_1&& \\ &d_2& \\ &&d_3 \end{bmatrix} \begin{bmatrix} 1&-1&0 \\ 0&1&-1 \\ 0&0&1 \end{bmatrix}

What must be true for A to be nonsingular?

(b) Given A above, assume we have a system of linear equations Ax = b with corresponding Lc = b as follows:

\begin{bmatrix} 1&0&0 \\ -1&1&0 \\ 0&-1&1 \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = b

Answer: (a) From the above we have A = LDU where L is a lower triangular matrix, D is a diagonal matrix, and U is an upper triangular matrix. Per p. 36 the diagonal entries of D are the pivots, and in order for A to be nonsingular all pivots must be nonzero. So A is nonsingular if and only if d_1, d_2, and d_3 are not zero.

(b) From above we have

b = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1&0&0 \\ -1&1&0 \\ 0&-1&1 \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} = \begin{bmatrix} c_1 \\ c_2-c_1 \\ c_3-c_2 \end{bmatrix} \Rightarrow c_1 = 0, c_2 = 0, c_3 = 1

Since A = LDU and Ax = b we have LDUx = b. But we also have Lc = b which implies DUx = c. Substituting from above this gives us

\begin{bmatrix} d_1&& \\ &d_2& \\ &&d_3 \end{bmatrix} \begin{bmatrix} 1&-1&0 \\ 0&1&-1 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}

Multiplying on the left gives us

\begin{bmatrix} d_1&-d_1&0 \\ 0&d_2&-d_2 \\ 0&0&d_3 \end{bmatrix} \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \Rightarrow d_1u-d_1v=0, d_2v-d_2w=0, d_3w=1

Assuming that none of d_1, d_2, and d_3 is zero, we then have

d_3w=1 \Rightarrow w = 1/d_3

d_2v-d_2w=0 \Rightarrow d_2v = d_2w \Rightarrow v = w = 1/d_3

d_1u-d_1v=0 \Rightarrow d_1u = d_1v \Rightarrow u = v = 1/d_3

So if A is nonsingular then Ax = b has the unique solution

x = \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} 1/d_3 \\ 1/d_3 \\ 1/d_3 \end{bmatrix}

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.8

Posted on January 9, 2011 by hecker

Exercise 1.5.8. This exercise continues the discussion in p. 33-34 regarding factorization of a 3×3 matrix A and the proof that A = LU. An alternative proof begins with the fact that row 3 of U is produced by taking row 3 of A and subtracting l_{31} times row 1 of U and l_{32} times row 2 of U. (Note that for simplicity we assume that no row exchanges are necessary.)

(a) Why do we subtract rows of U rather than rows of A?

(b) The above equation can be rearranged and restated as follows: row 3 of A is equal to the sum of l_{31} times row 1 of U, l_{32} times row 2 of U, and 1 times row 3 of U. Which rule of multiplication (from 1D on p. 25) makes this also equal to row 3 of LU?

Note that applying the results of (a) and (b) for the other rows of U completes the proof.

Answer: (a) By the time we apply elimination to row 3 of A we have already completed the elimination steps for rows 1 and 2 of A. The first step produced row 1 of U, and the second step produced row 2 of U. When we come to the elimination step for row 3 we are therefore subtracting multiples of rows of U, not rows of A.

By similar logic when performing an elimination step on any pivot row we have completed elimination on all the rows above it, and therefore any row subtracted from the pivot row (using the appropriate multiplier) is a row of U.

(b) From 1D part (iii) we have each row of the product matrix AB equal to the product of a row and a matrix; more specifically, row i of AB is equal to row i of A times the matrix B.

So for the product matrix LU we have row 3 of LU equal to row 3 of L times the matrix U.

Now we have

L = \begin{bmatrix} 1&0&0 \\ l_{21}&1&0 \\ l_{31}&l_{32}&1 \end{bmatrix}

so that row 3 of L consists of the entries l_{31}, l_{32}, and 1, and since U is upper triangular we have

U = \begin{bmatrix} u_{11}&u_{12}&u_{13} \\ 0&u_{22}&u_{23} \\ 0&0&u_{33} \end{bmatrix}

The product of row 3 of L and the matrix U (which is also row 3 of the product LU) is therefore

LU = \begin{bmatrix} l_{31}&l_{32}&1 \end{bmatrix} = \begin{bmatrix} u_{11}&u_{12}&u_{13} \\ 0&u_{22}&u_{23} \\ 0&0&u_{33} \end{bmatrix} = \begin{bmatrix} l_{31}u_{11}&l_{31}u_{12}+l_{32}u_{22}&l_{31}u_{13}+l_{32}u_{23}+u_{33} \end{bmatrix}

which can be expressed as

l_{31} \begin{bmatrix} u_{11}&u_{12}&u_{13} \end{bmatrix} + l_{32} \begin{bmatrix} 0&u_{22}&u_{23} \end{bmatrix} + 1 \cdot \begin{bmatrix} 0&0&u_{33} \end{bmatrix}

But this is l_{31} times row 1 of U plus l_{32} times the row 2 of U plus 1 times row 3 of U, and from above we have this equal to row 3 of A. Therefore row 3 of LU is equal to row 3 of A.

By similar arguments we show that row 1 of LU is equal to row 1 of A, and row 2 of LU is equal to row 2 of A. Since each row of LU is equal to the corresponding row of A, we have A = LU.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.7

Posted on January 8, 2011 by hecker

Exercise 1.5.7. Given the following lower triangular matrices

F = \begin{bmatrix} 1&&& \\ 2&1&& \\ 0&0&1& \\ 0&0&0&1\end{bmatrix} \quad G = \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&2&1& \\ 0&0&0&1\end{bmatrix} \quad H = \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&0&1& \\ 0&0&2&1\end{bmatrix}

find FGH and HGF.

Answer: We have FGH = (FG)H where

FG = \begin{bmatrix} 1&&& \\ 2&1&& \\ 0&0&1& \\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&2&1& \\ 0&0&0&1 \end{bmatrix} = \begin{bmatrix} 1&&& \\ 2&1&& \\ 0&2&1& \\ 0&0&0&1 \end{bmatrix}

so that

(FG)H = \begin{bmatrix} 1&&& \\ 2&1&& \\ 0&2&1& \\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&0&1& \\ 0&0&2&1 \end{bmatrix} = \begin{bmatrix} 1&&& \\ 2&1&& \\ 0&2&1& \\ 0&0&2&1 \end{bmatrix}

We also have HGF = (HG)F where

HG = \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&0&1& \\ 0&0&2&1 \end{bmatrix} \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&2&1& \\ 0&0&0&1 \end{bmatrix} = \begin{bmatrix} 1&&& \\ 0&1&&& \\ 0&2&1& \\ 0&4&2&1 \end{bmatrix}

so that

(HG)F = \begin{bmatrix} 1&&& \\ 0&1&& \\ 0&2&1& \\ 0&4&2&1 \end{bmatrix} \begin{bmatrix} 1&&& \\ 2&1&& \\ 0&0&1& \\ 0&0&0&1 \end{bmatrix} = \begin{bmatrix} 1&&& \\ 2&1&& \\ 4&2&1& \\ 8&4&2&1 \end{bmatrix}

Thus FGH \ne HGF.

UPDATE: Corrected the calculation of HGF; thanks go to Brian D. for pointing out my mistake.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.6

Posted on January 7, 2011 by hecker

Exercise 1.5.6. Given the matrix

E = \begin{bmatrix} 1&0 \\ 6&1 \end{bmatrix}

find E^2, E^8, and E^{-1}.

Answer: We have

E^2 = \begin{bmatrix} 1&0 \\ 6&1 \end{bmatrix} \begin{bmatrix} 1&0 \\ 6&1 \end{bmatrix} = \begin{bmatrix} 1&0 \\ 12&1 \end{bmatrix}

We can square this again to obtain

E^4 = E^2E^2 = \begin{bmatrix} 1&0 \\ 12&1 \end{bmatrix} \begin{bmatrix} 1&0 \\ 12&1 \end{bmatrix} = \begin{bmatrix} 1&0 \\ 24&1 \end{bmatrix}

and again to obtain

E^8 = E^4E^4 = \begin{bmatrix} 1&0 \\ 24&1 \end{bmatrix} \begin{bmatrix} 1&0 \\ 24&1 \end{bmatrix} = \begin{bmatrix} 1&0 \\ 48&1 \end{bmatrix}

In compting E^2 we note that all the entries match those of the identity matrix except for the 2,1 entry, which is 6 \cdot 1 + 1 \cdot 6 or 12. If we change the second 6 to -6 we instead obtain 6 \cdot 1 + 1 \cdot (-6) or zero for the 2,1 position. We then have

\begin{bmatrix} 1&0 \\ 6&1 \end{bmatrix} \begin{bmatrix} 1&0 \\ -6&1 \end{bmatrix} = \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} = I

so that

E^{-1} = \begin{bmatrix} 1&0 \\ -6&1 \end{bmatrix}

Another approach to finding E^{-1} is simply to note that E is an elementary matrix, and that its inverse therefore consists of the same matrix with the multiplier 6 negated.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.5

Posted on January 6, 2011 by hecker

Exercise 1.5.5. Given the following system of linear equations

Ax = \begin{bmatrix} 2&3&3 \\ 0&5&7 \\ 6&9&8 \end{bmatrix} \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ 5 \end{bmatrix} = b

find the factors L and U of A and the vector c for which Ux = c.

Answer: The 2,1 position of A is already zero, so there’s no need for an elimination step to make it zero. We then subtract 3 times the first row from the third, which makes the first two entries in the third row zero and produces the upper triangular matrix U:

\begin{bmatrix} 2&3&3 \\ 0&5&7 \\ 6&9&8 \end{bmatrix} \Rightarrow \begin{bmatrix} 2&3&3 \\ 0&5&7 \\ 0&0&-1 \end{bmatrix} = U

We then have L as the identity matrix with zero in the 2,1 position, 3 in the 3,1 position, and zero in the 3,2 position:

L = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 3&0&1 \end{bmatrix}

so that

LU = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 3&0&1 \end{bmatrix} \begin{bmatrix} 2&3&3 \\ 0&5&7 \\ 0&0&-1 \end{bmatrix} = \begin{bmatrix} 2&3&3 \\ 0&5&7 \\ 6&9&8 \end{bmatrix} = A

We then apply the same elimination steps to the righthand vector b, multiplying the first element by 3 and subtracting it from the third element:

\begin{bmatrix} 2 \\ 2 \\ 5 \end{bmatrix} \Rightarrow \begin{bmatrix} 2 \\ 2 \\ -1 \end{bmatrix}

producing the upper triangular triangular system Ux = c:

\begin{bmatrix} 2&3&3 \\ 0&5&7 \\ 0&0&-1 \end{bmatrix} \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} 2 \\ 2 \\ -1 \end{bmatrix}

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.4

Posted on January 5, 2011 by hecker

Exercise 1.5.4. Given the matrices

A = \begin{bmatrix} 2&1 \\ 8&7 \end{bmatrix} \quad A = \begin{bmatrix} 3&1&1 \\ 1&3&1 \\ 1&1&3 \end{bmatrix} \quad A = \begin{bmatrix} 1&1&1 \\ 1&4&4 \\ 1&4&8 \end{bmatrix}

use elimination to find the factors L and U for each of the matrices.

Answer: For the first matrix we subtract 4 times the first row from the second to obtain U:

\begin{bmatrix} 2&1 \\ 8&7 \end{bmatrix} \Rightarrow \begin{bmatrix} 2&1 \\ 0&3 \end{bmatrix} = U

The other factor L then is the identity matrix with 4 in the 2,1 position:

L = \begin{bmatrix} 1&0 \\ 4&1 \end{bmatrix}

so that

A = LU = \begin{bmatrix} 1&0 \\ 4&1 \end{bmatrix} \begin{bmatrix} 2&1 \\ 0&3 \end{bmatrix} = \begin{bmatrix} 2&1 \\ 8&7 \end{bmatrix}

For the second matrix we multiply the first row by 1/3 and subtract it from the second row, and also multiply the first row by 1/3 and subtract it from the second row:

\begin{bmatrix} 3&1&1 \\ 1&3&1 \\ 1&1&3 \end{bmatrix} \Rightarrow \begin{bmatrix} 3&1&1 \\ 0&\frac{8}{3}&\frac{2}{3} \\ 0&\frac{2}{3}&\frac{8}{3} \end{bmatrix}

We can multiply the second row of the resulting matriix by 1/4 and subtract it from the third row to obtain the upper triangular matrix U:

\begin{bmatrix} 3&1&1 \\ 0&\frac{8}{3}&\frac{2}{3} \\ 0&\frac{2}{3}&\frac{8}{3} \end{bmatrix} \Rightarrow \begin{bmatrix} 3&1&1 \\ 0&\frac{8}{3}&\frac{2}{3} \\ 0&0&\frac{5}{2} \end{bmatrix} = U

The other factor L then is the identity matrix with 1/3 in the 2,1 and 3,1 positions and 1/4 in the 3,2 position:

L = \begin{bmatrix} 1&0&0 \\ \frac{1}{3}&1&0 \\ \frac{1}{3}&\frac{1}{4}&1 \end{bmatrix}

so that

LU = \begin{bmatrix} 1&0&0 \\ \frac{1}{3}&1&0 \\ \frac{1}{3}&\frac{1}{4}&1 \end{bmatrix} \begin{bmatrix} 3&1&1 \\ 0&\frac{8}{3}&\frac{2}{3} \\ 0&0&\frac{5}{2} \end{bmatrix} = \begin{bmatrix} 3&1&1 \\ 1&3&1 \\ 1&1&3 \end{bmatrix} = A

For the third matrix we multiply the first row by 1 and subtract it from the second and third rows:

\begin{bmatrix} 1&1&1 \\ 1&4&4 \\ 1&4&8 \end{bmatrix} \Rightarrow \begin{bmatrix} 1&1&1 \\ 0&3&3 \\ 0&3&7 \end{bmatrix}

and then multiply the second row of the resulting matrix by 1 and subtract it from the third row to obtain the upper triangular matrix U:

\begin{bmatrix} 1&1&1 \\ 0&3&3 \\ 0&3&7 \end{bmatrix} \Rightarrow \begin{bmatrix} 1&1&1 \\ 0&3&3 \\ 0&0&4 \end{bmatrix} = U

The other factor L then is the identity matrix with 1 in the 2,1 and 3,1 positions and 1 in the 3,2 position as well:

L = \begin{bmatrix} 1&0&0 \\ 1&1&0 \\ 1&1&1 \end{bmatrix}

so that

LU = \begin{bmatrix} 1&0&0 \\ 1&1&0 \\ 1&1&1 \end{bmatrix} \begin{bmatrix} 1&1&1 \\ 0&3&3 \\ 0&0&4 \end{bmatrix} = \begin{bmatrix} 1&1&1 \\ 1&4&4 \\ 1&4&8 \end{bmatrix} = A

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.3

Posted on January 4, 2011 by hecker

Exercise 1.5.3. From equations (6) and (3) respectively we have

L = E^{-1}F^{-1}G^{-1} = \begin{bmatrix} 1&0&0 \\ 2&1&0 \\ -1&-1&1 \end{bmatrix} \quad GFE = \begin{bmatrix} 1&0&0 \\ -2&1&0 \\ -1&1&1 \end{bmatrix}

Multiply the two matrices, in both orders. Explain the two answers.

Answer: We have

\begin{bmatrix} 1&0&0 \\ 2&1&0 \\ -1&-1&1 \end{bmatrix} \begin{bmatrix} 1&0&0 \\ -2&1&0 \\ -1&1&1 \end{bmatrix} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix}

and

\begin{bmatrix} 1&0&0 \\ -2&1&0 \\ -1&1&1 \end{bmatrix} \begin{bmatrix} 1&0&0 \\ 2&1&0 \\ -1&-1&1 \end{bmatrix} = \begin{bmatrix} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix}

In other words, the product of the matrices is the same in both cases, and is the identity matrix I. This can be explained in two ways:

First, GFE is the matrix that embodies the elimination steps to take the matrix A to the upper triangular matrix U, while L takes U back to A: (GFE)A = U and LU = A. So applying GFE to A followed by L will take us back to A:

(E^{-1}F^{-1}G^{-1})(GFE)A = (E^{-1}F^{-1}G^{-1})U = LU = A

Thus (E^{-1}F^{-1}G^{-1})(GFE) is the identity matrix I.

Similarly, applying L to U followed by GFE takes us back to U:

(GFE)(E^{-1}F^{-1}G^{-1})U = (GFE)LU = (GFE)A = U

Thus (GFE)(E^{-1}F^{-1}G^{-1}) is also the identity matrix I.

Second, from the definition of the inverse of a matrix and the associative property of matrix multiplication we have

(E^{-1}F^{-1}G^{-1})(GFE) = (E^{-1}F^{-1})(G^{-1}G)(FE) = (E^{-1}F^{-1})I(FE) = (E^{-1}F^{-1})(FE) = E^{-1}(F^{-1}F)E = E^{-1}IE = E^{-1}E = I

and

(GFE)(E^{-1}F^{-1}G^{-1}) = (GF)(EE^{-1})(F^{-1}G^{-1}) = (GF)I(F^{-1}G^{-1}) = (GF)(F^{-1}G^{-1}) = G(FF^{-1})G^{-1} = GIG^{-1} = GG^{-1} = I

Thus

(E^{-1}F^{-1}G^{-1})(GFE) = (GFE)(E^{-1}F^{-1}G^{-1}) = I

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.2

Posted on January 3, 2011 by hecker

Exercise 1.5.2. Assume we have a matrix A with

A = \begin{bmatrix} 1&0&0 \\ 2&1&0 \\ 1&4&1 \end{bmatrix} \begin{bmatrix} 5&7&8 \\ 0&2&3 \\ 0&0&6 \end{bmatrix}

What multiple of row 2 of A will elimination subtract from row 3? What will be the pivots? Will a row exchange be required?

Answer: We have A = LU where L is a lower triangular matrix and U an upper triangular matrix:

L = \begin{bmatrix} 1&0&0 \\ 2&1&0 \\ 1&4&1 \end{bmatrix} \quad U = \begin{bmatrix} 5&7&8 \\ 0&2&3 \\ 0&0&6 \end{bmatrix}

The multipliers l_{ij} are the entries below the diagonal of L, with l_{ij} being the multiplier that multiplies the pivot row when it is subtracted from row i, and that produces a zero in the i, j position. Since in the exercise we are subtracting from row 3 we have i = 3, and since we are multiplying row 2 we have j = 2. The multiplier is therefore l_{32} or 4.

The pivots are the diagonal entries of U, or 5, 2, and 6.

There is no permutation matrix P present, so no row exchanges are required.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.5.1

Posted on January 2, 2011 by hecker

Exercise 1.5.1. Given an upper triangular matrix A, under what conditions is A nonsingular?

Answer: If A is upper triangular then the diagonal entries of A are the pivots of the corresponding system of linear equations. For A to be nonsingular then all the pivots must be nonzero. (If even one pivot is zero then A is singular, since A is already in upper triangular form and thus the zero pivot cannot be rectified using a row exchange.)

So A is nonsingular if and only if a_{ij} \ne 0 for all i, j.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, exercise 1.4.24

Posted on August 17, 2010 by hecker

Exercise 1.4.24. The following matrices can be multiplied using block multiplication, with the indicated submatrices within the matrices multiplied together:

\begin{bmatrix} x&x&\vline&x \\ x&x&\vline&x \\ \hline x&x&\vline&x \end{bmatrix} \begin{bmatrix} x&x&\vline&x \\ x&x&\vline&x \\ \hline x&x&\vline&x \end{bmatrix} \quad \rm or \quad \begin{bmatrix} x&x&\vline&x&x \\ x&x&\vline&x&x \end{bmatrix} \begin{bmatrix} x&x \\ x&x \\ \hline x&x \\ x&x \end{bmatrix}

  1. Provide example matrices matching the templates above and use block multiplication to multiply them together.
  2. Provide two example templates for multiplying a 3×4 matrix A and 4×2 matrix B using block multiplication.

Answer: (a) For the first example we multiply the following matrices using block multiplication on the indicated submatrices:

\begin{bmatrix} 1&2&\vline&3 \\ 2&1&\vline&2 \\ \hline 1&2&\vline&1 \end{bmatrix} \begin{bmatrix} 4&6&\vline&1 \\ 2&3&\vline&2 \\ \hline 1&5&\vline&3 \end{bmatrix}

To do block multiplication we must multiply all submatrices that are capable of being multiplied, i.e., the number of columns in the first submatrix is equal to the number of columns rows in the second submatrix. We then take the product of each pair of submatrices, assign it a spot in the final product matrix, and sum the resulting matrices to get the answer.

In the above example we start by multiplying the upper left 2×2 submatrix in the first matrix with the upper left 2×2 submatrix in the second matrix:

\begin{bmatrix} 1&2&\vline& \\ 2&1&\vline& \\ \hline &&\vline& \end{bmatrix} \begin{bmatrix} 4&6&\vline& \\ 2&3&\vline& \\ \hline &&\vline& \end{bmatrix} = \begin{bmatrix} 8&12&\vline& \\ 10&15&\vline& \\ \hline &&\vline& \end{bmatrix}

and then with the upper right 2×1 submatrix in the second matrix:

\begin{bmatrix} 1&2&\vline& \\ 2&1&\vline& \\ \hline &&\vline& \end{bmatrix} \begin{bmatrix} &&\vline&1 \\ &&\vline&2 \\ \hline &&\vline& \end{bmatrix} = \begin{bmatrix} &&\vline&5 \\ &&\vline&4 \\ \hline &&\vline& \end{bmatrix}

We next multiply the 2×1 upper right submatrix in the first matrix with the 1×2 lower left submatrix in the second matrix:

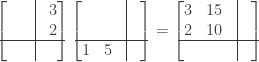
\begin{bmatrix} &&\vline&3 \\ &&\vline&2 \\ \hline &&\vline& \end{bmatrix} \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 1&5&\vline& \end{bmatrix} = \begin{bmatrix} 3&15&\vline& \\ 2&10&\vline& \\ \hline &&\vline& \end{bmatrix}

and then with the 1×1 lower right submatrix in the second matrix:

\begin{bmatrix} &&\vline&3 \\ &&\vline&2 \\ \hline &&\vline& \end{bmatrix} \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&3 \end{bmatrix} = \begin{bmatrix} &&\vline&9 \\ &&\vline&6 \\ \hline &&\vline& \end{bmatrix}

We next multiply the lower left 1×2 submatrix in the first matrix with the upper left 2×2 submatrix in the second matrix:

\begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 1&2&\vline& \end{bmatrix} \begin{bmatrix} 4&6&\vline& \\ 2&3&\vline& \\ \hline &&\vline& \end{bmatrix} = \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 8&12&\vline& \end{bmatrix}

and then with the upper right 2×1 submatrix in the second matrix:

\begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 1&2&\vline& \end{bmatrix} \begin{bmatrix} &&\vline&1 \\ &&\vline&2 \\ \hline &&\vline& \end{bmatrix} = \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&5 \end{bmatrix}

Finally we multiple the 1×1 submatrix in the lower right of the first matrix with the 1×2 submatrix in the lower left of the second matrix:

\begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&1 \end{bmatrix} \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 1&5&\vline& \end{bmatrix} = \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 1&5&\vline& \end{bmatrix}

and with the 1×1 submatrix in the lower right of the second matrix:

\begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&1 \end{bmatrix} \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&3 \end{bmatrix} = \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&3 \end{bmatrix}

Then we add all of the resulting matrices together:

\begin{bmatrix} 8&12&\vline& \\ 10&15&\vline& \\ \hline &&\vline& \end{bmatrix} + \begin{bmatrix} &&\vline&5 \\ &&\vline&4 \\ \hline &&\vline& \end{bmatrix} + \begin{bmatrix} 3&15&\vline& \\ 2&10&\vline& \\ \hline &&\vline& \end{bmatrix}

+ \begin{bmatrix} &&\vline&9 \\ &&\vline&6 \\ \hline &&\vline& \end{bmatrix} + \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 8&12&\vline& \end{bmatrix} + \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&5 \end{bmatrix}

+ \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline 1&5&\vline& \end{bmatrix} + \begin{bmatrix} &&\vline& \\ &&\vline& \\ \hline &&\vline&3 \end{bmatrix} = \begin{bmatrix} 11&27&\vline&14 \\ 12&25&\vline&10 \\ \hline 9&17&\vline&8 \end{bmatrix}

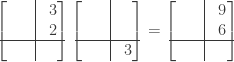
and compare to the result of conventional matrix multiplication:

\begin{bmatrix} 1&2&3 \\ 2&1&2 \\ 1&2&1 \end{bmatrix} \begin{bmatrix} 4&6&1 \\ 2&3&2 \\ 1&5&3 \end{bmatrix} = \begin{bmatrix} 4+4+3&6+6+15&1+4+9 \\ 8+2+2&12+3+10&2+2+6 \\ 4+4+1&6+6+5&1+4+3 \end{bmatrix} = \begin{bmatrix} 11&27&14 \\ 12&25&10 \\ 9&17&8 \end{bmatrix}

For the second example we multiply the following matrices using block multiplication on the indicated submatrices:

\begin{bmatrix} 1&2&\vline&4&2 \\ 3&4&\vline&3&5 \end{bmatrix} \begin{bmatrix} 3&5 \\ 1&2 \\ \hline 7&6 \\ 1&2 \end{bmatrix}

We start by multiplying the left 2×2 submatrix in the first matrix with the upper 2×2 submatrix in the second matrix:

\begin{bmatrix} 1&2&\vline&& \\ 3&4&\vline&& \end{bmatrix} \begin{bmatrix} 3&5 \\ 1&2 \\ \hline & \\ & \end{bmatrix} = \begin{bmatrix} 5&9 \\ 13&23 \end{bmatrix}

and then multiply the right 2×2 submatrix in the first matrix with the lower 2×2 submatrix in the second matrix:

\begin{bmatrix} &&\vline&4&2 \\ &&\vline&3&5 \end{bmatrix} \begin{bmatrix} & \\ & \\ \hline 7&6 \\ 1&2 \end{bmatrix} = \begin{bmatrix} 30&28 \\ 26&28 \end{bmatrix}

Then we add the two resulting matrices together:

\begin{bmatrix} 5&9 \\ 13&23 \end{bmatrix} + \begin{bmatrix} 30&28 \\ 26&28 \end{bmatrix} = \begin{bmatrix} 35&37 \\ 39&51 \end{bmatrix}

and compare to the result of conventional matrix multiplication:

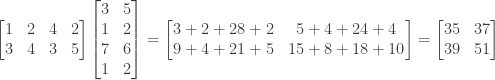
\begin{bmatrix} 1&2&4&2 \\ 3&4&3&5 \end{bmatrix} \begin{bmatrix} 3&5 \\ 1&2 \\ 7&6 \\ 1&2 \end{bmatrix} = \begin{bmatrix} 3+2+28+2&5+4+24+4 \\ 9+4+21+5&15+8+18+10 \end{bmatrix} = \begin{bmatrix} 35&37 \\ 39&51 \end{bmatrix}

(b) In multiplying a 3×4 matrix by a 4×2 matrix using block multiplication, one possible way to divide the matrices is as follows:

\begin{bmatrix} x&x&\vline&x&x \\ x&x&\vline&x&x \\ x&x&\vline&x&x \end{bmatrix} \begin{bmatrix} x&x \\ x&x \\ \hline x&x \\ x&x \end{bmatrix}

This results in multiplying the left 3×2 submatrix of the first matrix by the upper 2×2 submatrix of the second matrix to produce a 3×2 matrix, and multiplying the right 3×2 submatrix of the first matrix by the lower 2×2 submatrix of the second matrix to produce a second 3×2 matrix. The two 3×2 matrices are then added to produce the final 3×2 product matrix.

Another slightly more complicated approach is as follows:

\begin{bmatrix} x&x&x&\vline&x \\ x&x&x&\vline&x \\ x&x&x&\vline&x \end{bmatrix} \begin{bmatrix} x&x \\ x&x \\ x&x \\ \hline x&x \end{bmatrix}

This results in multiplying the left 3×3 submatrix of the first matrix by the upper 3×2 submatrix of the second matrix to produce a 3×2 matrix, and multiplying the right 3×1 submatrix of the first matrix by the lower 1×2 submatrix of the second matrix to produce a second 3×2 matrix. The two 3×2 matrices are then added to produce the final 3×2 product matrix.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment