My Math Homework

Definition of a block diagonal matrix

Posted on June 19, 2011 by hecker

This and subsequent posts continue the discussion in my previous post about multiplying block matrices. In this series of posts I consider block diagonal matrices and in particular how to partition an existing matrix into block diagonal form. I’m doing this both to gain a better understanding of what it means to have a block diagonal matrix, and also as background for a subsequent post discussing how to multiply and invert block diagonal matrices.

First, what is a block diagonal matrix? As defined by the relevant Wikipedia article, A block diagonal matrix is a block matrix which is a square matrix, and having [as] main diagonal blocks square matrices, such that the off-diagonal blocks are zero matrices.

Wolfram Mathworld provides a similar definition: A block diagonal matrix, also called a diagonal block matrix, is a square diagonal matrix in which the diagonal elements are square matrices of any size (possibly even 1×1), and the off-diagonal elements are 0. A block diagonal matrix is therefore a block matrix in which the blocks off the diagonal are the zero matrices, and the diagonal matrices are square.

Here’s another definition of block diagonal form consistent with the above definitions; it uses partition in the same sense as in my previous post on multiplying block matrices.

Let $A$ be an $n$ by $n$ square matrix, and suppose we partition $A$ into submatrices with $q$ row and column partitions:

$A = \begin{bmatrix} A_{11}&A_{12}&\cdots&A_{1q} \\ A_{21}&A_{22}&\cdots&A_{2q} \\ \vdots&\vdots&\ddots&\vdots \\ A_{q1}&A_{q2}&\cdots&A_{qq} \end{bmatrix}$

Thus partitioned, $A$ is a block diagonal matrix (or, alternately, has been partitioned into block diagonal form) if $A_{\alpha \beta} = 0, \alpha \ne \beta$ .

Note that by convention we consider any square matrix $A$ to be in block diagonal form with a single partition, i.e., when $q = 1$ . (This follows from the Wolfram Mathworld definition above, which defines a block diagonal matrix as a special type of diagonal matrix, and also from the Wolfram Mathworld definition of a diagonal matrix, which allows it to have just one element.)

We could stop with this definition and then proceed to derive the results of multiplying or inverting block diagonal matrices using the formula above. However in this series of posts I have tried to take a more rigorous approach (though I have probably failed to achieve full rigor in some areas of the argument). In particular I was interested in the question of how to best partition a matrix into block diagonal form, and felt it was important to address the fine details in order to convince myself that the informal approach was actually correct.

By convention a matrix $A$ is trivially in block diagonal form if considered to have a single partition, and a diagonal matrix $A$ is also in block diagonal form as well, with each entry on the diagonal considered as a submatrix with a single entry. What about the in-between cases though? Is there a canonical way to partition an arbitrary matrix so that it could (depending on its values) have multiple submatrices on the diagonal, with each submatrix having multiple entries?

I therefore want to prove a more definitive statement:

For any $n$ by $n$ square matrix $A$ we can uniquely and maximally partition $A$ into a block diagonal matrix with $r^2$ submatrices, for some $r$ where $1 \le r \le n$ , such that

$A = \begin{bmatrix} A_{11}&A_{12}&\cdots&A_{1r} \\ A_{21}&A_{22}&\cdots&A_{2r} \\ \vdots&\vdots&\ddots&\vdots \\ A_{r1}&A_{r2}&\cdots&A_{rr} \end{bmatrix} \qquad A_{\alpha \beta} = 0 \text{ if } \alpha \ne \beta$

This partitioning is maximal in the sense that $A$ cannot also be partitioned as a block diagonal matrix with $s$ partitions, where $s > r$ .

This partitioning is unique in the sense that if we partition $A$ into block diagonal form as

$A = \begin{bmatrix} A_{1}&0&\cdots&0 \\ 0&A_{2}&\cdots&0 \\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\cdots&A_{r} \end{bmatrix}$

and also into block diagonal form as

$A = \begin{bmatrix} A'_{1}&0&\cdots&0 \\ 0&A'_{2}&\cdots&0 \\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\cdots&A'_{r} \end{bmatrix}$

then $A_{\alpha} = A'_{\alpha}, 1 \le \alpha \le r$ .

In the next post I start the process of trying to prove the above statement, by constructing a way to partition $A$ as described.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | 2 Comments

Linear Algebra and Its Applications, Exercise 1.6.18

Posted on May 19, 2011 by hecker

Exercise 1.6.18. Suppose that

$A = L_1D_1U_1 = L_2D_2U_2$

Show that

$L_1 = L_2 \quad D_1 = D_2 \quad U_1 = U_2$

Answer: We have

$L_1D_1U_1 = L_2D_2U_2 \rightarrow L_1^{-1}L_1D_1U_1 = L_1^{-1}L_2D_2U_2 \rightarrow D_1U_1 = L_1^{-1}L_2D_2U_2$

$\rightarrow D_1U_1 U_2^{-1} = L_1^{-1}L_2D_2U_2U_2^{-1} \rightarrow D_1U_1 U_2^{-1} = L_1^{-1}L_2D_2$

The product of two upper triangular matrices is also an upper triangular matrix, and multiplying by a diagonal matrix preserves this. The left side of the final equation above is therefore an upper triangular matrix. Similarly the product of two lower triangular matrices is also an lower triangular matrix, and multiplying by a diagonal matrix does not change this. The right side of the final equation above is therefore an lower triangular matrix.

In order for both of these things to be true, the left and right hand sides of the final equation above must therefore both equal some diagonal matrix D:

$D_1U_1 U_2^{-1} = L_1^{-1}L_2D_2 = D$

Now, since $D_1$ is a diagonal matrix and D is also a diagonal matrix, the product $U_1U_2^{-1}$ must also be a diagonal matrix. If it were not, and had at least one entry

$u_{ij} \ne 0, i \ne j$

then the (i, j) entry of D would be equal to the product of the nonzero (i, i) entry of $D_1$ and the nonzero (i, j) entry of $U_1U_2^{-1}$ and would therefore be nonzero itself. But this is a contradiction since D is a diagonal matrix, so the product $U_1U_2^{-1}$ must be a diagonal matrix.

Also, by definition $U_1$ and $U_2$ have ones on the diagonal. Since $U_2$ is an upper triangular matrix with ones on the diagonal, its inverse (which is also an upper triangular matrix, as shown in exercise 1.16.12) must have ones on the diagonal as well, as shown by the following argument:

Let $U_2$ have entries $u_{ij}$ and $U_2^{-1}$ have entries $v_{ij}$ . Since $U_2U_2^{-1} = I$ , for the (i, i) entry of $U_2U_2^{-1}$ we therefore have

$\sum_k u_{ik}v_{ki} = 1$

But since both $U_1$ and $U_2^{-1}$ are upper triangular we have

$u_{ik} = 0, k < i$

and

$v_{ki} = 0, k > i$

so that

$1 = \sum_k u_{ik}v_{ki} = u_{ii}v_{ii} = v_{ii}$

since $U_1$ has ones on the diagonal.

Since both $U_1$ and $U_2^{-2}$ are upper triangular matrices with ones on the diagonal, their product $U_1U_2^{-1}$ also has ones on the diagonal. But we also know that this product is a diagonal matrix, so that we then have

$U_1U_2^{-1} = I \rightarrow U_1 = U_2$

since $U_1$ has a unique inverse.

A similar argument shows that

$L_1^{-1}L_2 = I \rightarrow L_1 = L_2$

We then have

$D_1U_1 U_2^{-1} = L_1^{-1}L_2D_2 \rightarrow D_1I = ID_2 \rightarrow D_1 = D_2$

and the factorization A = LDU is therefore unique.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

If you find these posts useful I encourage you to also check out the more current Linear Algebra and Its Applications, Fourth Edition, Dr Strang’s introductory textbook Introduction to Linear Algebra, Fourth Edition and the accompanying free online course, and Dr Strang’s other books.

Posted in linear algebra | Leave a comment

Linear Alegbra and Its Applications, Exercise 1.6.17

Posted on May 18, 2011 by hecker

Exercise 1.6.17. (a) Suppose that the n by n matrix A can be factored as LDU, where L and U have ones on the diagonal. Factor the transpose of A.

(b) If we have

$A^Ty = b$

what triangular systems will provide a solution?

Answer: (a) Since A can be factored as LDU we have

$A^T = (LDU)^T = U^T(LD)^T = U^T(D^TL^T) = U^TDL^T$

(Note that D is its own transpose.)

Since U is upper triangular its transpose is lower triangular, and since L is lower triangular its transpose is upper triangular. We thus have the factorization

$A^T = U^TDL^T$

(b) Since $A^T$ can be factored as shown above, we have

$A^Ty = b \rightarrow U^TDL^Ty = b \rightarrow U^Tc = b \ \rm and \ DL^Ty = c$

These are the two triangular systems as requested.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in Uncategorized | Leave a comment

Linear Algebra and Its Applications, Exercise 1.6.16

Posted on May 17, 2011 by hecker

Exercise 1.6.16. (i) If A is an n by n symmetric matrix, how many entries of A can be chosen independently of each other?

(ii) If If K is an n by n skew-symmetric matrix, how many entries of K can be chosen independently?

Answer: (i) Since A is an n by n matrix, it has $n^2$ entries. We can select n independent entries to go on the diagonal, leaving $n^2 - n$ off-diagonal entries to be chosen. However since A is a symmetric matrix only half of those entries (e.g., those above the diagonal) can be chosen independently, since the corresponding entries in the other part of the matrix (in this case, below the diagonal) will be the same.

The total number of independent entries is then

$n + (n^2 - n)/2 = (2n + n^2 - n)/2 = (n^2 + n)/2 = n(n+1)/2$

(ii) Even though K is skew-symmetric rather than symmetric, the entries below the diagonal are still dependent on the corresponding entries above the diagonal. (They’re simply negatives of those entries rather than being the same.) The number of off-diagonal entries that can be chosen independently is thus the same as for A.

However for a skew-symmetric matrix $K = -K^T$ we must have $k_{ii} = -k_{ii}$ for all $i$ , so that all the entries on the diagonal must be zero. Since the entries on the diagonal cannot be chosen independently, the number of independent entries is just half the number of off-diagonal entries, or

$(n^2 - n)/2 = n(n-1)/2$

UPDATE: Corrected the answer to part (ii) to account for the diagonal entries being zero.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in linear algebra | 2 Comments

Linear Algebra and Its Applications, Exercise 1.16.15

Posted on May 16, 2011 by hecker

Exercise 1.6.15. For any square matrix B and matrices A and K where

$A = B + B^T, \quad K = B - B^T$

prove that A is symmetric and K is skew-symmetric, i.e.,

$K^T = -K$

For the case where

$B = \begin{bmatrix} 1&3 \\ 1&1 \end{bmatrix}$

compute A and K and show that B can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix.

Answer: Let $C = B^T$ . For all elements of A we then have

$a_{ij} = b_{ij} + c_{ij} = c_{ji} + b_{ji} = b_{ji} + c_{ji} = a_{ji}$

so that

$A = A^T$

and A is a symmetric matrix.

For all elements of K we have

$k_{ij} = b_{ij} - c_{ij} = c_{ji} - b_{ji} = -(b_{ji} - c_{ji}) = -k_{ji}$

so that

$K^T = -K$

and K is a skew-symmetric matrix.

We then have

$B = \begin{bmatrix} 1&3 \\ 1&1 \end{bmatrix} \quad B^T = \begin{bmatrix} 1&1 \\ 3&1 \end{bmatrix}$

so that

$A = B + B^T = \begin{bmatrix} 1&3 \\ 1&1 \end{bmatrix} + \begin{bmatrix} 1&1 \\ 3&1 \end{bmatrix} = \begin{bmatrix} 2&4 \\ 4&2 \end{bmatrix}$

and

$K = B - B^T = \begin{bmatrix} 1&3 \\ 1&1 \end{bmatrix} - \begin{bmatrix} 1&1 \\ 3&1 \end{bmatrix} = \begin{bmatrix} 0&2 \\ -2&0 \end{bmatrix}$

Note that

$A + K = (B + B^T) + (B - B^T) = B + B + B^T - B^T = 2B$

so that

$B = \frac{1}{2}(A + K)$

In our example we then have

$\begin{bmatrix} 1&3 \\ 1&1 \end{bmatrix} = \frac{1}{2}(\begin{bmatrix} 2&4 \\ 4&2 \end{bmatrix} + \begin{bmatrix} 0&2 \\ -2&0 \end{bmatrix})$

$= \frac{1}{2} \begin{bmatrix} 2&4 \\ 4&2 \end{bmatrix} + \frac{1}{2} \begin{bmatrix} 0&2 \\ -2&0 \end{bmatrix} = \begin{bmatrix} 1&2 \\ 2&1 \end{bmatrix} + \begin{bmatrix} 0&1 \\ -1&0 \end{bmatrix}$

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.6.14

Posted on May 15, 2011 by hecker

Exercise 1.6.14. For any m x n matrix A, prove that $AA^T$ and $A^TA$ are symmetric matrices. Provide an example where these matrices are not equal.

Answer: Per Equation 1M(i) on page 47 we have

$(AB)^T = B^TA^T$

Substituting $A^T$ for B we have

$(AA^T)^T = (A^T)^TA^T = AA^T$

Since $AA^T$ is equal to its own transpose it is a symmetric matrix.

Similarly we have

$(A^TA)^T = A^T(A^T)^T = A^TA$

Since $A^TA$ is equal to its own transpose it too is a symmetric matrix.

Next, we pick an example 2 x 2 matrix

$A = \begin{bmatrix} 1&2 \\ 1&3 \end{bmatrix}$

We then have

$AA^T = \begin{bmatrix} 1&2 \\ 1&3 \end{bmatrix} \begin{bmatrix} 1&1 \\ 2&3 \end{bmatrix} = \begin{bmatrix} 5&7 \\ 7&10 \end{bmatrix}$

and

$A^TA = \begin{bmatrix} 1&1 \\ 2&3 \end{bmatrix} \begin{bmatrix} 1&2 \\ 1&3 \end{bmatrix} = \begin{bmatrix} 2&5 \\ 5&13 \end{bmatrix}$

So in general $AA^T$ does not equal $A^TA$ .

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in Uncategorized | Leave a comment

Linear Algebra and Its Applications, Exercise 1.16.13

Posted on May 14, 2011 by hecker

Exercise 1.6.13. Compute $A^TB$ , $B^TA$ , $AB^T$ , and $BA^T$ for the following matrices:

$A = \begin{bmatrix} 3 \\ 1 \end{bmatrix} \quad B = \begin{bmatrix} 2 \\ 2 \end{bmatrix}$

Answer: We have

$A^TB = \begin{bmatrix} 3&1 \end{bmatrix} \begin{bmatrix} 2 \\ 2 \end{bmatrix} = 8$

$B^TA = \begin{bmatrix} 2&2 \end{bmatrix} \begin{bmatrix} 3 \\ 1 \end{bmatrix} = 8$

$AB^T = \begin{bmatrix} 3 \\ 1 \end{bmatrix} \begin{bmatrix} 2&2 \end{bmatrix} = \begin{bmatrix} 6&6 \\ 2&2 \end{bmatrix}$

$BA^T = \begin{bmatrix} 2 \\ 2 \end{bmatrix} \begin{bmatrix} 3&1 \end{bmatrix} = \begin{bmatrix} 6&2 \\ 6&2 \end{bmatrix}$

Note that per Equation 1M(i) on page 47 we have

$(AB)^T = B^TA^T$

This means that

$(A^TB)^T = B^T(A^T)^T = B^TA$

and

$(AB^T)^T = (B^T)^TA^T = BA^T$

as confirmed by the computation above.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.6.12

Posted on May 13, 2011 by hecker

Exercise 1.6.12. Suppose that A is an invertible matrix and has one of the following properties:

(1) A is a triangular matrix.

(2) A is a symmetric matrix.

(3) A is a tridiagonal matrix.

(4) All the entries of A are whole numbers.

(5) All the entries of A are rational numbers (i.e., fractions or whole numbers).

Which of the above would also be true of the inverse of A? Prove your conclusions or find a counterexample if false.

Answer: (1) Assume that A is an invertible triangular matrix. A can be either upper triangular or lower triangular. We first assume that A is upper triangular, such that

$a_{ij} = 0, i > j$

We use Gauss-Jordan elimination to find the inverse of A. Since A is upper triangular forward elimination is complete, since all entries beneath the diagonal of A are already zero. (Moreover, the diagonal entries of A are nonzero, since if there were any zeros in the pivot position A would be singular and hence not invertible.)

We can thus proceed immediately to backward elimination. The first backward elimination step multiplies all entries in the last row and subtracts them from the next-to-last row. But we still have I on the righthand side, and I has all zero entries below the diagonal just as A does. We will be multiplying zero entries below the diagonal of the right-hand matrix (i.e., in the last row), and then subtracting the resulting zero values from other zero values below the diagonal of the right-hand side (i.e., in the next to last row). As a result, after the first backward elimination step all the entries below the diagonal of the right-hand matrix will still be zero.

By similar reasoning the second step of backward elimination will also produce zero entries below the diagonal of the right-hand matrix, and so will each subsequent step. When Gauss-Jordan backward elimination finally completes, the final right-hand matrix, which is the inverse of A, will thus have all zero entries below the diagonal and will be upper triangular. Thus if A is upper triangular and invertible then the inverse of A will be upper triangular as well.

Now suppose A is invertible and lower triangular, so that

$a_{ij} = 0, i < j$

Again we do Gauss-Jordan elimination to find the inverse of A. The first forward elimination step multiplies all entries in the first row and subtracts them from the second row. We will be multiplying zero entries above the diagonal of both the left-hand and the right-hand matrix (i.e., in the first row), and then subtracting the resulting zero values from other zero values above the diagonal of the left-hand and the right-hand matrix (i.e., in the second row). As a result, after the first forward elimination step all the entries above the diagonal of both the left-hand and the right-hand matrix will still be zero.

By similar reasoning the second step of forward elimination will also produce zero entries above the diagonal of both the left-hand and right-hand matrix, and so will each subsequent step. After forward elimination completes both the lefthand matrix and the righthand matrix will thus have zeroes above the diagonal. Since the lefthand matrix has all zeroes above the diagonals there is no need to do backward elimination, and all that remains is to divide both matrices by the values in the pivot positions.

This division will leave any zero entries still zero, so the final righthand matrix, i.e., the inverse of A, will also have zeroes above the diagonal and will be lower triangular. Thus if A is lower triangular and invertible then the inverse of A will be lower triangular as well. Combining these two results, if A is an invertible triangular matrix then the inverse of A is triangular as well.

(2) Suppose that A is an invertible symmetric matrix. Since A is symmetric we have

$A^T = A$

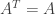
and since A is invertible we have

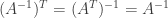
$(A^{-1})^T = (A^T)^{-1} = A^{-1}$

But since the inverse of A is equal to its own transpose it is a symmetric matrix. Thus if A is an invertible symmetric matrix then the inverse of A is also symmetric.

(3) We attempt to find a counter-example by constructing a 4 by 4 tridiagonal matrix A such that:

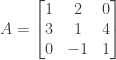
$A = \begin{bmatrix} 1&2&0 \\ 3&1&4 \\ 0&-1&1 \end{bmatrix}$

and then use Gauss-Jordan elimination to find its inverse:

$A = \begin{bmatrix} 1&2&0&1&0&0 \\ 3&1&4&0&1&0 \\ 0&-1&1&0&0&1 \end{bmatrix} \rightarrow \begin{bmatrix} 1&2&0&1&0&0 \\ 0&-5&4&-3&1&0 \\ 0&-1&1&0&0&1 \end{bmatrix}$

$\rightarrow \begin{bmatrix} 1&2&0&1&0&0 \\ 0&-5&4&-3&1&0 \\ 0&0&\frac{1}{5}&\frac{3}{5}&-\frac{1}{5}&1 \end{bmatrix} \rightarrow \begin{bmatrix} 1&2&0&1&0&0 \\ 0&-5&0&-15&5&-20 \\ 0&0&\frac{1}{5}&\frac{3}{5}&-\frac{1}{5}&1 \end{bmatrix}$

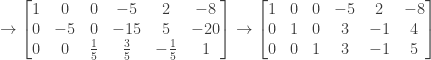
$\rightarrow \begin{bmatrix} 1&0&0&-5&2&-8 \\ 0&-5&0&-15&5&-20 \\ 0&0&\frac{1}{5}&\frac{3}{5}&-\frac{1}{5}&1 \end{bmatrix} \rightarrow \begin{bmatrix} 1&0&0&-5&2&-8 \\ 0&1&0&3&-1&4 \\ 0&0&1&3&-1&5 \end{bmatrix}$

We therefore have

$A^{-1} = \begin{bmatrix} -5&2&-8 \\ 3&-1&4 \\ 3&-1&5 \end{bmatrix}$

which is not a tridiagonal matrix. Therefore if A is an invertible tridiagonal matrix it is not necessarily the case that the inverse of A is also tridiagonal.

(4) We attempt to find a counter-example by constructing a 2 by 2 matrix A with whole number entries:

$A = \begin{bmatrix} 1&0 \\ 0&3 \end{bmatrix}$

We then have

$A^{-1} = \begin{bmatrix} 1&0 \\ 0&\frac{1}{3} \end{bmatrix}$

which does not have whole number entries. Therefore if A is an invertible matrix whose entries are all whole numbers, it is not necessarily the case that all the entries of the inverse of A are also whole numbers.

(5) Suppose that A is an invertible matrix and that all of the entries of A are rational numbers (whole numbers or fractions). For each i and j the corresponding entry of A is thus of the form

$a_{ij} = p/q$

where p is some integer and q is some non-zero integer. (If q is 1 then the entry is a whole number.)

We use Gauss-Jordan elimination to find the inverse of A, and without loss of generality assume that no row exchanges are required for the first step. The first forward elimination step multiplies all entries in the first row and subtracts the results from each of the remaining rows, with the multipliers for each row being computed as the pivot in the first row divided by each of the entries in the same column of the remaining rows (assuming those entries are nonzero).

But a rational number divided by a nonzero rational number is itself a rational number, as is a rational number multiplied by another rational number, and as is a rational number added to or subtracted from another rational numbers. (See below for the proof of this.) Since all the entries in A are rational numbers, as are all in the entries in I (the right-hand matrix for the first elimination step), all the entries in the left-hand and right-hand matrices resulting from the first forward elimination step are also rational numbers.

By similar reasoning the second forward elimination step will produce only rational numbers, as will any subsequent elimination step. Similarly backward elimination will produce only rational numbers at each step, as will the final division by the nonzero pivots. The right-hand matrix after the final step, i.e., the inverse of A, thus has all entries being rational numbers. So if A is an invertible matrix with all rational entries then the inverse of A will also have all rational entries.

Proof that the product, sum, and difference of two rational numbers are themselves rational numbers, as is the result of dividing a rational number by a nonzero rational number:

Let a and b be rational numbers. We then have

$a = p/q, b = r/s$

for some p, q, r, and s where p and r are integers and q and s are nonzero integers.

The product of a and b is then

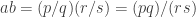
$ab = (p/q)(r/s) = (pq)/(rs)$

Since p and q are both integers their product is an integer, and since r and s are both nonzero integers their product is also a nonzero integer. The product of a and b can thus be expressed as an integer divided by a nonzero integer, and thus is a rational number.

The sum of a and b is then

$a + b = (p/q) + (r/s) = (ps/qs) + (qr/qs) = (ps + qr)/qs$

The product of p and s is an integer, as is the product of q and r, and thus their sum is an integer as well. Also, since q and s are nonzero integers their product is a nonzero integer as well. The sum of a and b can thus be expressed as an integer divided by a nonzero integer, and thus is a rational number.

The difference of a and b can be show to be a rational number by a similar argument.

Finally, if b is nonzero then a divided by b is

$a/b = (p/q)/(r/s) = (p/q)(s/r) = (ps)/(qr)$

Since p and s are integers their product is an integer as well. We also have q as a nonzero integer and since b is nonzero r is also a nonzero integer, so that the product of q and r is a nonzero integer as well. The result of dividing a by b can thus be expressed as an integer divided by a nonzero integer, and thus is a rational number.

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in linear algebra | Leave a comment

Linear Algebra and Its Applications, Exercise 1.6.11

Posted on April 9, 2011 by hecker

Exercise 1.6.11. For each of the following criteria, give examples of matrices A and B that satisfy the criteria:

(i) Both A and B are invertible, but their sum A+B is not invertible.

(ii) Neither A nor B is invertible, but their sum A+B is invertible.

(iii) A, B, and their sum A+B are all invertible.

For (iii), in addition show that $B^{-1} + A^{-1}$ is also invertible, and find an expression for its inverse. Hint: use the fact that

$A^{-1}(A + B)B^{-1} = B^{-1} + A^{-1}$

Answer: (i) I is the simplest example of an invertible matrix, being its own inverse. If I is flipped horizontally to form a matrix like the first example in exercise 1.6.10, that matrix is also invertible, and like I is its own inverse. So we can choose

$A = \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} = A^{-1}, B = \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix} = B^{-1}$

but

$A+B = \begin{bmatrix} 1&1 \\ 1&1 \end{bmatrix}$

which is not invertible.

(ii) If we modify the matrix A in (i) by removing the top left entry of 1 then we obtain a matrix that is not invertible, ditto if we remove the bottom right entry. We can therefore choose A and B as follows:

$A = \begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix}, B = \begin{bmatrix} 1&0 \\ 0&0 \end{bmatrix}$

These are not invertible, but their sum is I which is invertible:

$A + B = \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} = (A + B)^{-1}$

(iii) A 2 by 2 matrix is invertible as long as (ad – bc) is nonzero. We can therefore again use I as our first matrix, and modify it slightly to obtain a second invertible matrix:

$A = \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix}, B = \begin{bmatrix} 1&0 \\ 0&2 \end{bmatrix}$

We then have

$A +B = \begin{bmatrix} 1&0 \\ 0&3 \end{bmatrix}$

which is also invertible. A is of course its own inverse, and we also have

$B^{-1} = \begin{bmatrix} 1&0 \\ 0&\frac{1}{2} \end{bmatrix}, (A + B)^{-1} = \begin{bmatrix} 1&0 \\ 0&\frac{1}{3} \end{bmatrix}$

Continuing, let’s first prove the formula that was given as a hint:

$A^{-1}(A + B)B^{-1} = (A^{-1}A + A^{-1}B)B^{-1} = (I + A^{-1}B)B^{-1}$

$= B^{-1} + A^{-1}BB^{-1} = B^{-1} + A^{-1}$

If A, B, and A+B are all invertible then we have the following:

$(B^{-1}+A^{-1}) B(A+B)^{-1}A = A^{-1}(A + B)B^{-1}B(A+B)^{-1}A$

$= A^{-1}(A + B)(A+B)^{-1}A = A^{-1}A = I$

and

$B(A+B)^{-1}A(B^{-1}+A^{-1}) = B(A+B)^{-1}AA^{-1}(A + B)B^{-1}$

$= B(A+B)^{-1}(A + B)B^{-1} = BB^{-1} = I$

so that

$(B^{-1}+A^{-1})^{-1} = B(A+B)^{-1}A$

NOTE: This continues a series of posts containing worked out exercises from the (out of print) book Linear Algebra and Its Applications, Third Edition by Gilbert Strang.

Posted in linear algebra | Leave a comment

Multiplying block matrices

Posted on April 7, 2011 by hecker

In doing exercise 1.6.10 in Linear Algebra and Its Applications I was reminded of the general issue of multiplying block matrices, including diagonal block matrices. This also came up in exercise 1.4.24 as well, which I answered without necessarily fully understanding the problem. I therefore wanted to go back and try to prove various claims about block matrices, starting with the following:

Let $A$ and $B$ be an $m$ by $p$ matrix and a $p$ by $n$ matrix respectively. Suppose we partition $A$ into submatrices with $q$ row partitions and $s$ column partitions:

$A = \begin{bmatrix} A_{11}&A_{12}&\cdots&A_{1s} \\ A_{21}&A_{22}&\cdots&A_{2s} \\ \vdots&\vdots&\ddots&\vdots \\ A_{q1}&A_{q2}&\cdots&A_{qs} \end{bmatrix}$

and we partition $B$ into submatrices with $s$ row partitions and $r$ column partitions:

$B = \begin{bmatrix} B_{11}&B_{12}&\cdots&B_{1r} \\ B_{21}&B_{22}&\cdots&B_{2r} \\ \vdots&\vdots&\ddots&\vdots \\ B_{s1}&B_{s2}&\cdots&B_{sr} \end{bmatrix}$

Show that the $m$ by $n$ matrix product $C = AB$ can be described as a block matrix with $q$ row partitions and $r$ column partitions

$C = \begin{bmatrix} C_{11}&C_{12}&\cdots&C_{1r} \\ C_{21}&C_{22}&\cdots&C_{2r} \\ \vdots&\vdots&\ddots&\vdots \\ C_{q1}&C_{q2}&\cdots&C_{qr} \end{bmatrix}$

with submatrices computed as follows:

$C_{\alpha \beta} = \sum_{\gamma = 1}^{s} A_{\alpha \gamma} B_{\gamma \beta}$

Proof: (Note that I’m sure a better proof of this exists, not to mention better notation. However this is the best I can come up with.)

We define a block matrix within $A$ as follows: First, we divide the $m$ rows of $A$ into $q$ partitions, where $1 \le q \le m$ . The partition is done using a vector $u$ of nonnegative integer values defined as follows:

$u = \begin{bmatrix} u_1&u_2&\cdots&u_{q+1} \end{bmatrix}$

$u_1 = 0, u_{q+1} = m$

$u_i < u_{i+1}, 1 \le i \le q$

This can be interpreted as follows: $u_i + 1$ is the first row in the $i^{th}$ partition, $u_{i+1}$ is the last row in the $i^{th}$ partition, and $u_{i+1} - u_i \ge 1$ is the number of rows in the $i^{th}$ partition.

We then divide the $p$ columns of $A$ into $s$ partitions, where $1 \le s \le p$ , using a vector $w$ of nonnegative integer values defined as follows:

$w = \begin{bmatrix} w_1&w_2&\cdots&w_{s+1} \end{bmatrix}$

$w_1 = 0, w_{s+1} = p$

$w_i < w_{i+1}, 1 \le i \le s$

The vector $w$ has a similar interpretation to the vector $u$ : $w_i + 1$ is the first column in the $i^{th}$ partition, $w_{i+1}$ is the last column in the $i^{th}$ partition, and $w_{i+1} - w_i \ge 1$ is the number of columns in the $i^{th}$ partition.

We then define $q$ times $s$ submatrices of $A$ , with a given submatrix defined in terms of the entries of $A$ as follows:

$A_{\alpha \beta} = \begin{bmatrix} a_{u_\alpha+1, w_\beta+1}&a_{u_\alpha+1,w_\beta + 2}&\cdots&a_{u_\alpha+1,w_{\beta+1}} \\ a_{u_\alpha+2, w_\beta+1}&a_{u_\alpha+2,w_\beta+2}&\cdots&a_{u_\alpha+2,w_{\beta+1}} \\ \vdots&\vdots&\ddots&\vdots \\ a_{u_{\alpha+1}, w_\beta+1}&a_{u_{\alpha+1},w_\beta+2}&\cdots&a_{u_{\alpha+1},w_{\beta+1}} \end{bmatrix}$

so that the $(i, j)$ entry of $A_{\alpha \beta}$ has the value

$(A_{\alpha \beta})_{ij} = a_{u_\alpha+i,w_\beta+j}$

Note that when $q = s = 1$ we have

$u = \begin{bmatrix} 0&m \end{bmatrix}, w = \begin{bmatrix} 0&p \end{bmatrix}$

so that

$A_{11} = \begin{bmatrix} a_{u_1+1,w_1+1}&a_{u_1+1,w_1 + 2}&\cdots&a_{u_1+1,w_2 } \\ a_{u_1 + 2, w_1+1}&a_{u_1 + 2,w_1 + 2}&\cdots&a_{u_1 + 2,w_2} \\ \vdots&\vdots&\ddots&\vdots \\ a_{u_2, w_1+1}&a_{u_2,w_1+2}&\cdots&a_{u_2,w_2} \end{bmatrix}$

$= \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1p} \\ a_{21}&a_{22}&\cdots&a_{2p} \\ \vdots&\vdots&\ddots&\vdots \\ a_{m1}&a_{m2}&\cdots&a_{mp} \end{bmatrix} = A$

In other words, in this case $A$ has only a single submatrix, namely $A$ itself.

Also note that when $q = m$ and $s = p$ we have

$u = \begin{bmatrix} 0&1&\cdots&m \end{bmatrix}, w = \begin{bmatrix} 0&1&\cdots&p \end{bmatrix}$

so that

$u_i = i-1, w_j = j-1$

We then have

$A_{\alpha \beta} = \begin{bmatrix} a_{u_\alpha+1, w_\beta+1}&\cdots&a_{u_\alpha+1,w_{\beta+1}} \\ \vdots&\vdots&\ddots&\vdots \\ a_{u_{\alpha+1}, w_\beta+1}&\cdots&a_{u_{\alpha+1},w_{\beta+1}} \end{bmatrix}$

$= \begin{bmatrix} a_{(\alpha-1)+1,(\beta-1)+1}&\cdots&a_{(\alpha-1)+1,(\beta+1)-1} \\ \vdots&\vdots&\ddots&\vdots \\ a_{(\alpha+1)-1,(\beta-1)+1}&\cdots&a_{(\alpha+1)-1,(\beta+1)-1} \end{bmatrix} = \begin{bmatrix} a_{\alpha \beta} \end{bmatrix}$

In other words, in this case $A$ has $m$ times $p$ submatrices, each containing a single entry of $A$ .

We next define a block matrix within $B$ as follows: First, we divide the $p$ rows of $B$ into $s$ partitions, using the same vector $w$ used to partition the columns of $A$ .

(Note: It is important that the rows of $B$ be partitioned in the exact same manner as the columns of $A$ , and not just that the number of partitions $s$ be the same. Otherwise we won’t be able to multiply submatrices of $A$ by the corresponding submatrices of $B$ , because the number of columns in a submatrix of $A$ won’t necessarily match the number of rows in the corresponding submatrix of $B$ . Unfortunately some references don’t make this clear, including at one point the block matrix article at Wikipedia.)

We then divide the $n$ columns of $B$ into $r$ partitions, where $1 \le r \le n$ , using a vector $v$ of nonnegative integer values defined as follows:

$v = \begin{bmatrix} v_1&v_2&\cdots&v_{r+1} \end{bmatrix}$

$v_1 = 0, v_{r+1} = n$

$v_i < v_{i+1}, 1 \le i \le r$

Again, the vector $v$ has the same interpretation as the vectors $u$ and $w$ : $v_i + 1$ is the first column in the $i^{th}$ partition, $v_{i+1}$ is the last column in the $i^{th}$ partition, and $v_{i+1} - v_i \ge 1$ is the number of columns in the $i^{th}$ partition.

We then define $s$ times $r$ submatrices of $B$ , with a given submatrix defined in terms of the entries of $B$ as follows:

$B_{\alpha \beta} = \begin{bmatrix} b_{w_\alpha+1 ,v_\beta+1}&b_{w_\alpha+1,v_\beta+2}&\cdots&b_{w_\alpha+1,v_{\beta+1}} \\ b_{w_\alpha+2, v_\beta+1}&b_{w_\alpha+2,v_\beta+2}&\cdots&b_{w_\alpha+2,v_{\beta+1}} \\ \vdots&\vdots&\ddots&\vdots \\ b_{w_{\alpha+1}, v_\beta+1}&b_{w_{\alpha+1},v_\beta+2}&\cdots&b_{w_{\alpha+1},v_{\beta+1}} \end{bmatrix}$

As in the case of $A$ , if $s = r = 1$ then there is only a single submatrix of $B$ , namely $B$ itself, and if $s = p$ and $r = n$ then each submatrix contains a single entry of $B$ . The $(i, j)$ entry of $B_{\alpha \beta}$ has the value

$(B_{\alpha \beta})_{ij} = b_{w_\alpha+i,v_\beta+j}$

Finally, consider the $m$ by $n$ matrix $C = AB$ with entries

$c_{ij} = \sum_{k=1}^p a_{ik}b_{kj}$

We can partition the rows of $C$ into $q$ partitions according to the same vector $u$ used to partition the rows of $A$ , and partition the columns of $C$ into $r$ partitions according to the same vector $v$ used to partition the columns of $B$ . We then have

$C_{\alpha \beta} = \begin{bmatrix} c_{u_\alpha+1, v_\beta+1}&c_{u_\alpha+1,v_\beta + 2}&\cdots&c_{u_\alpha+1,v_{\beta+1}} \\ c_{u_\alpha+2, v_\beta+1}&c_{u_\alpha+2,v_\beta+2}&\cdots&c_{u_\alpha+2,v_{\beta+1}} \\ \vdots&\vdots&\ddots&\vdots \\ c_{u_{\alpha+1}, v_\beta+1}&c_{u_{\alpha+1},v_\beta+2}&\cdots&c_{u_{\alpha+1},v_{\beta+1}} \end{bmatrix}$

with the $(i, j)$ entry of $C_{\alpha \beta}$ having the value

$(C_{\alpha \beta})_{ij} = c_{u_\alpha+i,v_\beta+j}$

Now consider the following matrix:

$D_{\alpha \beta} = \sum_{\gamma = 1}^{s} A_{\alpha \gamma} B_{\gamma \beta}$

for some $\alpha$ and $\beta$ where $1 \le \alpha \le q$ and $1 \le \beta \le r$ .

First, note that all the submatrices $A_{\alpha \gamma}$ have $u_{\alpha+1} - u_\alpha$ rows and $w_{\gamma+1} - w_\gamma$ columns, and all the submatrices $B_{\gamma \beta}$ have $w_{\gamma+1} - w_\gamma$ rows and $v_{\beta+1} - v_\beta$ columns. (This follows from the definitions of $u$ , $w$ , and $v$ .)

Since the number of columns in the submatrices $A_{\alpha \gamma}$ is the same as the number of rows in the submatrices $B_{\gamma \beta}$ , matrix multiplication is possible, and the resulting product matrices will have $u_{\alpha+1} - u_\alpha$ rows and $v_{\beta+1} - v_\beta$ columns. Since $D_{\alpha \beta}$ is the sum of the product matrices, it too will have $u_{\alpha+1} - u_\alpha$ rows and $v_{\beta+1} - v_\beta$ columns, the same number of rows and columns as $C_{\alpha \beta}$ (based on the partitioning of $C$ as described above).

Now consider the $(i, j)$ entry in $D_{\alpha \beta}$ . It will consist of the sum of all the $(i, j)$ entries in the product matrices. More formally,

$(D_{\alpha \beta})_{ij} = \sum_{\gamma = 1}^{s} (A_{\alpha \gamma} B_{\gamma \beta})_{ij}, 1 \le i \le u_{\alpha+1} - u_\alpha, 1 \le j \le v_{\beta+1} - v_\beta$

Since the number of columns in the submatrices $A_{\alpha \gamma}$ and the number of rows in the submatrices $B_{\gamma \beta}$ is $w_{\gamma+1} - w_\gamma$ , we then have

$(A_{\alpha \gamma} B_{\gamma \beta})_{ij} = \sum_{l=1}^{w_{\gamma+1} - w_\gamma} (A_{\alpha \gamma})_{il} (B_{\gamma \beta})_{lj}$

$= \sum_{l=1}^{w_{\gamma+1} - w_\gamma} a_{u_\alpha+i,w_\gamma+l}b_{w_\gamma+l,v_\beta+j} = \sum_{k=w_\gamma+1}^{w_{\gamma+1}} a_{u_\alpha+i,k}b_{k,v_\beta+j}$

so that

$(D_{\alpha \beta})_{ij} = \sum_{\gamma = 1}^{s} \sum_{k=w_\gamma+1}^{w_{\gamma+1}} a_{u_\alpha+i,k}b_{k,v_\beta+j}$

Note that the first inner sum (when $\gamma = 1$ ) starts at $k = 1$ (because $w_1 = 0$ by definition), that each subsequent inner sum starts at a value of $k$ one greater than the last, and that the last inner sum (when $\gamma = s$ ) ends at $k = p$ (because $w_{s+1} = p$ ). We thus conclude that $k$ takes on all values from 1 to $p$ , and only those values, so that we can rewrite the above as

$(D_{\alpha \beta})_{ij} = \sum_{k=1}^{p} a_{u_\alpha+i,k}b_{k,v_\beta+j} = c_{u_\alpha+i,v_\beta+j} = (C_{\alpha \beta})_{ij}$

Since $D_{\alpha \beta}$ and $C_{\alpha \beta}$ have the same number of rows and columns (as discussed above), and since the $(i, j)$ entry of $D_{\alpha \beta}$ is equal to the $(i, j)$ entry of $C_{\alpha \beta}$ for all $i$ and $j$ , we conclude that $C_{\alpha \beta} = D_{\alpha \beta}$ , and from the definition of $D$ that

$C_{\alpha \beta} = \sum_{\gamma = 1}^{s} A_{\alpha \gamma} B_{\gamma \beta}$

which was what we set out to prove.

Note that if $q = s = r = 1$ then

$A_{11} = A, B_{11} = B, C_{11} = C$

so that the above equation reduces to $C = AB$ .

On the other hand, if $q = m$ , $s = p$ , and $r = n$ then we have

$A_{\alpha \beta} = \begin{bmatrix} a_{\alpha \beta} \end{bmatrix}$

$B_{\alpha \beta} = \begin{bmatrix} b_{\alpha \beta} \end{bmatrix}$

$C_{\alpha \beta} = \begin{bmatrix} c_{\alpha \beta} \end{bmatrix}$

so that the equation

$C_{\alpha \beta} = \sum_{\gamma = 1}^{s} A_{\alpha \gamma} B_{\gamma \beta}$

is essentially equivalent to

$c_{\alpha \beta} = \sum_{\gamma = 1}^{s} a_{\alpha \gamma} b_{\gamma \beta}$

UPDATE: Since originally writing this post I slightly changed the definition of a partitioning vector $v$ . First, I clarified that $v$ contained nonnegative integer entries. Second, I used the condition $v_i < v_{i+1}$ instead of $v_i < v_j$ for $i < j$ , because I think it better corresponds to the intuitive idea of how a partition would be defined.

Note that we can derive the old condition from the new one:

Suppose $v_i < v_{i+1}$ for $1 \le i \le q$ and we have $v_j$ with $j > i$ . Let $l = j-i \ge 1$ . We have $v_i < v_{i+k}$ when $k = 1$ . (This is the new condition that we are assuming is true.) Now suppose $v_i < v_{i+k}$ for some $k \ge 1$ . We have $v_{i+k} < v_{(i+k)+1}$ based on the new condition (assuming that $(i+k) \le q$ so that $v_{(i+k)+1}$ has a value), so $v_i < v_{i+k}$ implies that $v_i < v_{i+(k+1)}$ .

By induction we then have $v_i < v_{i+k}$ for all $k \ge 1$ for which $v_{i+k}$ has a value. Since $l = j - i \ge 1$ and $v_{i+l}$ has a value (since $v_j = v_{i+l}$ does) we then have $v_i < v_{i+l} = v_j$ . Thus $v_i < v_{i+1}$ for $1 \le i \le q$ implies that for any $v_i$ and $v_j$ we have $v_i < v_j$ if $j > i$ .

Also, since $i+1 > i$ , the old condition that $v_i < v_j$ for $j > i$ implies the new condition that $v_i < v_{i+1}$ . Thus the old and new conditions are equivalent, and the choice between them in defining a partitioning vector is simply a matter of convenience.

Buy me a snack to sponsor more posts like this!

Posted in linear algebra | 6 Comments

My Math Homework

Definition of a block diagonal matrix

Linear Algebra and Its Applications, Exercise 1.6.18

Linear Alegbra and Its Applications, Exercise 1.6.17

Linear Algebra and Its Applications, Exercise 1.6.16

Linear Algebra and Its Applications, Exercise 1.16.15

Linear Algebra and Its Applications, Exercise 1.6.14

Linear Algebra and Its Applications, Exercise 1.16.13

Linear Algebra and Its Applications, Exercise 1.6.12

Linear Algebra and Its Applications, Exercise 1.6.11

Multiplying block matrices

Archives

Meta